网友提问:为什么行星轨道都是椭圆的?为什么太阳只集中在一个焦点上,那么另一个焦点又是什么呢?
答:这个问题总是困扰着我。简短回答一下:这个问题从数学上超纲了,尤其是在第一年的物理学和微积分范围外。事实上太阳在一个焦点是个再正常不过的事儿,更常见的是,另一个焦点什么也没有。

仅凭直觉很难回答为什么星轨是椭圆的。实际上我也没找到一个数学推理可以回答这个问题。所以,我把推导过程留在答案区里。

答案区:重力一般被写为:

你可以引入矢量符号重写为:

这里上面的点表示时间导数。为了保证标准:


C为“整数常量”,可以是任何一个数字。
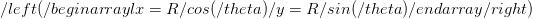
在极坐标系下,你可以用半径(远离或靠近太阳的速度)及角度(转动的速度)来重新定义速度。


L是这个问题中行星的角动量,是一个常数。虽然看起来有点蠢,但是为了预测,在推理中我们最好用1/R来代替R.

P和e的选择看起来有一点武断,不过这些有些历史意义。P为半通径,可以说是用来描述轨道大小的。E为离心率,描述了轨道的椭圆程度,e=0意味着轨道为圆形,在0-1只见为椭圆,<=1则意味着轨道未闭合(这种情况实际上不能称之为“轨道”)。比如,地球轨道的离心率为0.01671123,哈雷彗星的离心率为0.967.

D仅描述了椭圆轨道远端的指向,实际上与形状无关。
所以仅有最后一个方程是定义了椭圆的,在这个系统中,(0,0)正好在一个圆心,一下即证据:
一个焦点在(0,0)点的椭圆可以被描述为:

F即中心至焦点的距离

这些合在一起,便能看出椭圆的形状(本例中即为太阳在(0,0)点)。

图片说明:一个小天体在太空中沿者椭圆路径的轨道绕着另一个大天体(像是行星绕着太阳),而这个大天体坐落在椭圆焦点上。
相关知识-开普勒定律在天文学中,开普勒定律是用于描述行星环绕太阳运动的定律。

行星轨道是椭圆的,第一个星球的焦点在F1\F2,第二个星球的焦点在F1\F3。太阳位于焦点F1。
阴影部分A1、A2有相同的表面积,对于行星1而言环绕A1和A2所需的时间相同。
行星A1和A2绕轨道一圈的时间为固定比例。
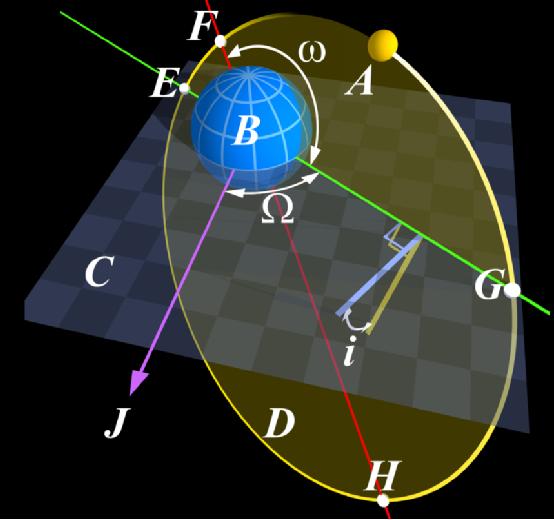
行星轨道是椭圆的,太阳位于其一个焦点上。
过太阳与行星的连线将椭圆分割成相等的两部分,且两部分的绕行时间相同。
绕行时间的平方与长半径的立方成比例。

图片说明:在此图中,右上象限的是椭圆轨道的重力井,在质量中心的重力位能井显示出位能,轨道速度的动能以红色显示。当轨道上天体的速度减少时动动也会减少,同时距离会遵循开普勒定律增加。
大多数的行星轨道都接近于圆形,只有通过细心观察缜密计算才能知道轨道其实是椭圆的。火星轨道经计算是椭圆的。从这一点出发,开普勒推断太阳系其他行星的轨道也都是椭圆的。
哥白尼的日心说已经解释了为何行星速度不同,在此基础上,开普勒用椭圆替代圆,将研究推进了一步。
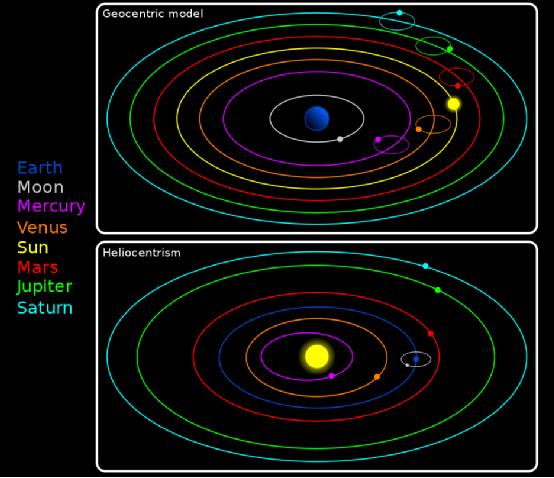
图片说明:地心说(上图)与日心说(下图)二者模型之比较
牛顿于1687年提出了更精确的解释,提出了运动定律及万有引力定律。
椭圆轨道在天文学或天体力学是轨道离心率小于1的开普勒轨道,包括特别的离心率为零的圆轨道。在严格的意义上,它是一个离心率大于0且小于1(因此不包括圆轨道)的开普勒轨道。在更广泛的意义上,它是一个包括负能量的开普勒轨道,这包括轨道离心率等于1的径向椭圆轨道(抛物线轨道)。
参考资料1.WJ百科全书
2.天文学名词
3. askamathematician- The Physicist
如有相关内容侵权,请于三十日以内联系作者删除
转载还请取得授权,并注意保持完整性和注明出处
,