对于傅里叶变换,其中的一些概念很容易让人模糊不清,比如,周期函数和非周期函数的傅里叶转换有什么不同,
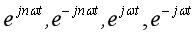
核函数
这四个核函数更是让人头痛不已,到底什么时候要负号,什么时候不要负号,什么时候有n,什么时候没有n。这篇文章就讨论一下这个问题。



我们先把这个证明的思路搞清楚:首先

也就是说,这里证明的是周期函数的傅里叶级数展开;然后我们再看一下这个证明的思路: 它首先是假设任何一个周期函数都可以展开为正弦函数之和,然后再求出各个正弦函数的系数,系数求出的过程也很简单,就是以正弦函数的周期

进行方程左右两边的积分,最后得出傅里叶级数的系数表达式。注意,是傅里叶级数,不是傅里叶变换。然后,上述结果可以写成:

接着,是利用欧拉公式将这个表达式转变成指数形式:
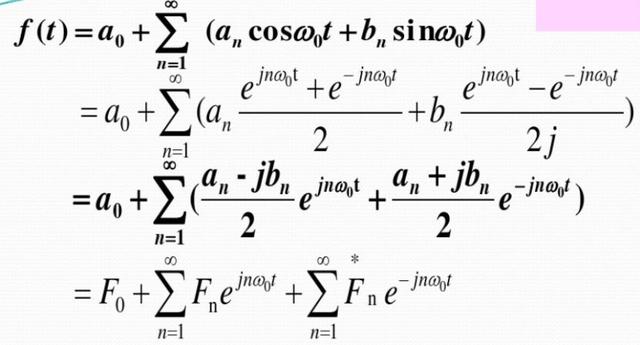


最后,f(t)可以合并写成:

上述转变过程很容易看懂,看懂以后,我们只要注意到:第一个表达式就是周期函数f(t)的指数傅里叶级数形式,其核函数里面有n,没有负号,这个表达式表示的是周期函数f(t)从时域到频域的级数展开过程;第二个表达式表示的是函数f(t)展开为傅里叶级数时的系数的求法,其核函数里面有n,也有负号。 接下来,就需要把周期函数转变成非周期函数,再求其傅里叶变换。这个转变过程更简单,就是假设
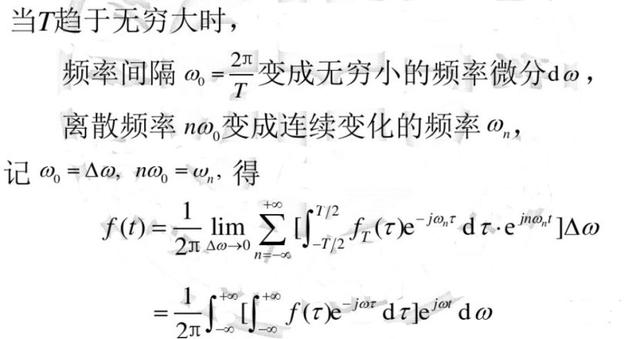
然后定义非周期函数的傅里叶变换

上述是定义,不用什么证明,我们注意到,这个时候核函数里面没有n,有负号,这是时域到频域的正向变换过程。那么对于非周期函数f(t),就有

这个时候核函数里面没有n,没有负号,这是频域到时域的逆向变换过程。 最后,我们把周期和非周期函数的傅里叶过程放在一起,总结一下:

从上面的分析可以总结如下:
1:周期函数对应于傅里叶级数,非周期函数对应傅里叶变换,两者之间的转化在于周期T是否是无穷大。
2:傅里叶级数中,核函数里面都有n;而傅里叶变换里面都没有;
3:无论傅里叶级数还是傅里叶变换,函数展开时(f(t)在方程左边),核函数都是正的;否则都是负的。
,




