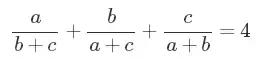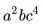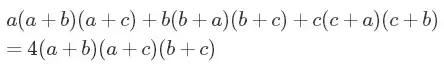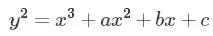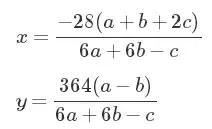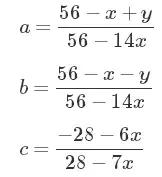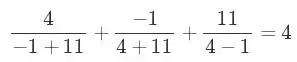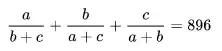看似侮辱智商
实则智商压制
这是一篇最近很火的文章。一个常见题目,貌似易解的题目出发,发现背后竟然蕴藏了深奥的大道理。这其实是很多问题,尤其是数论题目的特点:很容易理解,但很难做。
作者:Alon Amit译者:镜子文明在我碰到这道题之前,它已经被某人心怀恶意地发布在网络上,成为流行的朋友圈图片,肆意捉弄那些老实人(Scridhar,这个人是不是你?)。我根本没意识到我偶然看到的这道题到底是个什么样的怪物。它长这个样:
你可能已经在朋友圈看到过很多这样的图了,它们一般都是标题党的垃圾:什么“95%的麻省理工毕业生无法解决的问题”,这个“问题”要么很空洞,要么偷换概念,要么就是不重要的脑筋急转弯。
但这个问题不是。这张图片就是一个精明的,或者说阴险的圈套。大概99.999995%的人根本没有任何机会解决它,甚至包括一大批顶级大学非数论方向的数学家。它的确是可解的,但那真的真的不得了的难。
(顺便说一句。发布的人实际上不是Scridhar,或者说不能怪他。)
你可能会这样想,如果所有的尝试都失败了,我们还可以直接用电脑计算大力出奇迹。这年头,写个电脑程序解决这种形式简单的方程真是太容易了,只要它真的有答案,那电脑最终一定会找出来。但很抱歉,大错特错。用电脑暴力计算在这里毫无用处。
如果不把Quora的读者都当作椭圆曲线的入门者的话,我不知道怎么才能写出适合的答案。我在这能做的只是一个简要的概览。主要参考文献是最近Bremmer和MacLeod2014年在《数学和信息学年鉴(Annales Mathematicae etInformaticae)》上发表的一篇名为《一个不一般的立体代表性问题(An unusual cubic representationproblem)》的精彩论文。
让我们开始吧。
我们求解的是这个方程的整数解:
(为了与论文的变量名相适应,我把苹果、香蕉和菠萝修改过来了)
面对任何方程,你需要做的第一步是尝试并确定问题背景。这到底被划归到哪一类问题?嗯,我们被要求找到整数解,所以这是一个数论问题。就题而言,方程涉及有理函数(多项式除多项式的函数形式),但很显然我们可以用通分移项的方法化成一个多项式函数,所以我们实际上解得是一个丢番图方程( Diophantine equation)。正数解的要求有一点不同寻常,接下来我们会看到这个要求会让问题变得多么难。
现在,我们有了多少变量?这个问题看起来很蠢:很明显,我们有三个变量,分别是a、b、c。让我们慢一点来。一个科班出身的数论学家第一眼就能察觉到,这个方程是齐次的。这意味着如果(a,b,c)是方程的一个特解的话,那(7a,7b,7c)都是它的解。你能看出为什么吗?给每一个变量乘一个常数没有改变方程的结构(7只是一个例子),因为分子分母全部都约掉了。
这意味着这个方程看上去像是三维的,但它实际上只有两维。在几何学中,它对应着一个面(一个三元方程一般定义一个两维的面。一般来说,k个n元方程定义一个d维的流形,d=n-k)。这个面是由一条过原点的线旋转形成的,可以通过截取的单平面来理解。这是一条投影曲线。
在大多数初等的情形,这种降维可以这么解释:无论解是什么,我们都可以分为两类,c=0的情形和c≠0的情形。第一类仅仅涉及两个变量(所以自然是二维的),而第二类情形我们可以对所有解同时除以c并得到一个c=1的解(注:在上上一段,我们已经说明了这样一组解也一定是方程的解)。因此我们可以在c=1的情况下寻找a和b的有理数解,只要乘以一个公分母,就得到了a,b,c的正数解。一般来说,齐次方程的整数解对应一个低一个维度的非齐次方程的有理数解。
接下来的问题是:这个方程的次数是什么?次数指的是各项中最高的幂次,对于涉及多个变量相乘的项,幂次就是各变量幂次之和。举个例子,如果某项为
,那此项的次数就是7=2 1 4 。
丢番图方程在不同次数难度完全不一样,宽泛地说:
一次的非常简单。二次的也被理解得非常透彻,一般能用相对初等的方法解决。三次的就是满山满海的深奥理论和数不胜数的开放问题。四次的,嗯,真的真的很难。我们这个方程是三次的。为什么?嗯,去分母之后就很显然了:
即使没有合并同类项,你也可以明白地看到次数为3:没有超过三个变量的乘积,最后我们得到的是类似a³ 、b²c、abc这样的项,而没有幂次超过3的。合并同类项后,方程整理如下
你可能会反对这样的变形:因为这样获得的解可能恰好使某个分母等于0,使得原方程没有意义。这是对的,我们的新方程的确有些解不与原方程对应。但这是好事。这个多项式形式给原方程打上了一些补丁使得它便于处理;对于我们找到的任何特解,只需要代入原方程检验一下分母等不等于0就可以了。
事实上,多项式方程很容易处理。比如说, a=−1 ,b=1, c=0。这是好事:我们有了有理数解,或者说有理点。这意味着我们的立体方程(3维)实际上是个椭圆曲线。
当你发现这个方程是椭圆曲线时,你会喜出望外,然后悲从中来(注:这里不是大家熟悉的圆锥曲线中的椭圆,而是域上亏格为1的光滑射影曲线。对于特征不等于2的域,它的仿射方程可以写成:y^2=x^3 ax^2 bx c。复数域上的椭圆曲线为亏格为1的黎曼面。Mordell证明了整体域上的椭圆曲线是有限生成交换群,这是著名的BSD猜想的前提条件。阿贝尔簇是椭圆曲线的高维推广。By 百度百科。),因为你发现椭圆曲线问题是个庞然大物(学渣哇的一声哭出来)。这个方程是一个展现椭圆曲线理论强大的经典案例,证明它可以被用来寻找一些爆难问题的解。
我们需要做的第一件事把椭圆曲线化成魏尔斯特拉斯(注:Weierstrass,提起他最著名的成就就是严密化微积分的ε-δ语言)形式。这是一个长得像这样的等式:
或者有时候也会化成
(这被称为长魏尔斯特拉斯形式。它并不是严格必需的,但有时候会带来一些便利)
众所周知,任何椭圆曲线都可以化成这种形式(在特征为2或者3的域特别基础,如果你研究特征特别小的域,那结果就不一样了,我们此处不作讨论)。如果想讲清楚怎么把椭圆曲线化成这种形式,那可就是长篇大论了(学渣的碎碎念:我信我信)。你只需要知道,这种变形是完全机械的操作(关键在于方程至少存在一个有理数点,而我们已经确定了一个有理数点)。现在有若干计算机函数包可以轻而易举地帮你搞定这件事。
但即使你不知道如何完成变换,验证它也是很容易的,或者说至少是机械的。对于我们而言,需要的变换由令人生畏的公式导出。
我知道这看上去就像随意的巫毒把戏(注:巫毒,是目前最为人熟悉的非洲信仰,在西方文化中就是神秘力量的象征符号,可以类比国人心中的毒盅、赶尸和降头),但请相信我它不是。一旦你完成了这些变形,沉闷但异常直白的代数计算可以证明它是对的。
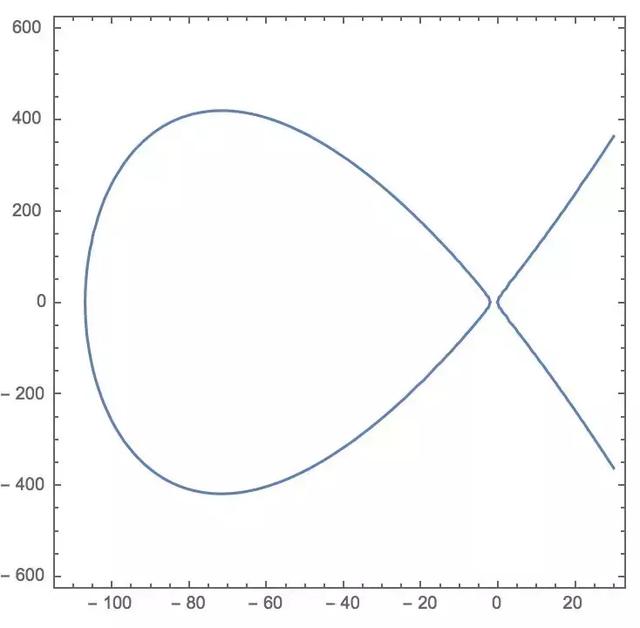
这个方程尽管看起来很原方程长得不怎么像,但确是如假包换的忠实模型。在图像上它长成这样,一条有着两个实部的经典椭圆曲线:
右边的“鱼尾”连续延伸至正负无穷。左边的封闭椭圆曲线也将给我们带来解决问题的惊喜。给定这个方程的任意解(x,y),你都可以通过下面的等式还原所求的a,b,c:
你需要记住,三元组(a:b:c)是用投影曲线理解的——无论你从这些方程中获得什么数值,你都可以随意乘上一个你想要的常数。
对于我们展示的两个图像,无论是从a,b,c到x,y还是反过来,都可以证明这两个方程从数论的角度是等价的:一个方程的有理数解可以导出另一个方程的有理数解。专业术语叫做双向有理等价(birational equivalence),而这个概念在代数几何里面是一个非常基本的。如我们之前注意到的那样,可能存在一些不相互对应的特殊点,而情形是a b,a c 或者b c恰好等于0 。这是构造双有理等价的必要代价,而不需要对此有任何担心。
让我们来看看手里的这个例子。它的椭圆曲线存在一个很好的有理数点:x=−100, y=260。可能找到这个点不太容易,但检验它在曲线上就很简单了:直接代入原方程检验等式两边是否相等(我不是随机摸的点,但各位不用关心这个问题)。我们可以简单地验证a,b,c代入的结果。
我们得到了a=2/7,b=−1/14,c=11/14,既然我们可以随意乘以一个公分母,那我们就可以变形为a=4,b=−1,c=11.
代入原方程,的确
你可以很容易地验证。这就是我们原方程的一个简单整数解——但很遗憾,不是正整数解。找到这个解用手算不太容易,但用一点耐心即使不用计算机也不算太难。它将成为我们找到正数解的缘起之地。
现在,一旦你在椭圆曲线上找到了有理数点,如P(-100,260),你就可以利用弦切技巧进行加法,生成其它的有理数点(有理数的加法是封闭的,有理数加有理数还是有理数)。
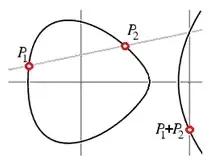
图解:椭圆曲线上点的加法
在任何情形下,在一个域(实数域R或者有理数域Q)中给定一个方程,解可以被视为位于R²或者Q²的点(来自R²或者Q²的投影),而相加律就是弦—切结构的变形:想要对两个点P₁和P₂做加法,首先构造一条过二点的直线(弦),若P₁,P₂重合,那么这条直线就是曲线的切线。找到直线与曲线的第三个交点P,对O和P重复上述操作,再次得到的交点就是P₁ P₂。当O点被选为无穷远处的点(一般都这么处理),图像就如上所示(注:至于O点是什么,这就涉及群论和更深奥的椭圆曲线知识,懂的自然懂,不懂的我也讲不懂,因为我也不懂)。更详细的见原作者的Quora回答previous,再详细的请去翻代数几何。
一开始,我们可以通过作P点的切线,找到它和曲线再次相交的点,以此增加P点的值。结果看上变得有点吓人:
同样的,这个新的点也对应一组a,b,c的值:
这个解用手算就很困难,但用电脑就是小意思了。然而,它还不是正的。
当然,困难吓不倒我们,我们继续计算3P=2P P,操作方法就是连接P和2P找到与曲线的第三个交点再与O点相连找到第四个交点。同样的,我们计算a,b,c,然而还是同样的,结果不是正数。以此类推,计算4P,5P等等等等。直到我们计算到9P。
9P=(-66202368404229585264842409883878874707453676645038225/13514400292716288512070907945002943352692578000406921,
58800835157308083307376751727347181330085672850296730351871748713307988700611210/1571068668597978434556364707291896268838086945430031322196754390420280407346469)
很明显这不是人算的了,但交给机器,这也就是9次简单的几何程序迭代。对应的a,b,c值也很恐怖:
a=154476802108746166441951315019919837485664325669565431700026634898253202035277999,
b=36875131794129999827197811565225474825492979968971970996283137471637224634055579,
c=4373612677928697257861252602371390152816537558161613618621437993378423467772036
这些是80位数!你不可能通过暴力计算找到一个80位数(注:简单的算术题,按确定两个变量验证第三个变量为整数的算法计算,总共的组合数就是10^160,神威太湖之光的峰值计算能力为12.5亿亿次每秒,折算不过10^18 次/s,至少需要10^142秒,大约10^134年,更震撼的写法就是1亿亿亿亿亿亿亿亿亿亿亿亿亿亿亿亿年)!但无论它看上去怎么不可思议,但这些数值代回原方程,的确等于4:
让我们回到理论本身再探讨一下。定义在有理数上的椭圆曲线存在一个阶(rank),它表示我们最开始至少需要知道多少个有理点才能通过弦切方法找到曲线上所有的有理数点。我们这条椭圆曲线的阶等于1,说明虽然它上面有无穷多个有理点但都是由一个有理点生成的,而这个点不是别的恰好就是我们最开始的那个P点(-100,260)。
计算阶数并找到这样的一个生成子的算法非同寻常,但SageMath(现在叫CoCalc)只需要几行代码1秒钟以内就搞定了。你可以查看我的代码,它从头开始再现了整个解法,当然其中有Sage内置的椭圆曲线处理方法。
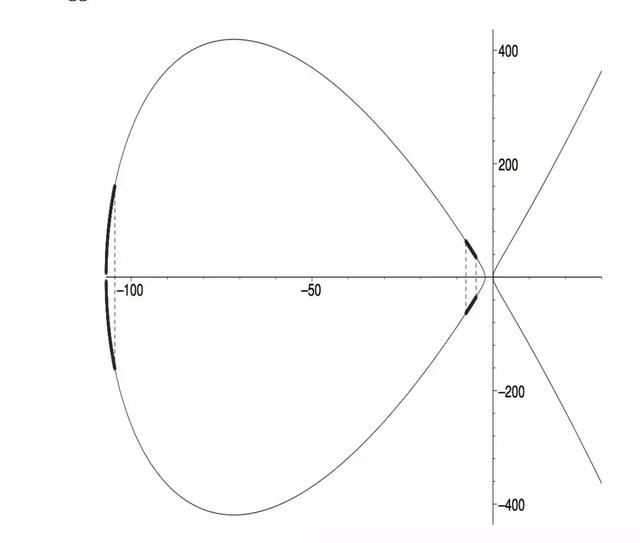
在我们看来,P点位于曲线的椭圆部分,而其它的mP(m为正整数)点也一样。它们会逐渐跑遍整个椭圆并最终均匀地分布在整个曲线上。而我们是很幸运的,因为只有很少一部分椭圆能产生a,b,c的正数解:它们是下面这张图加粗的部分(引自Bremmer和MacLeod的论文)。
P,2P等点并不在黑色加粗的部分,但9P恰好在,使我们得到一个80位的正整数解。
Bremmer和MacLeod还研究了如果我们把等式右边的4换成其它的东西会怎么样。如果你觉得我们的解太大了,那是因为你还没见识到把4换成178的结果。那就不仅仅是80位了,你需要398,605,460位数。对,你没看错,那个解就是这么大。如果你试试896,位数就飙升到数万亿位了。没错,数万亿位的解,属于这个看上去人畜无害的方程。
述的丢番图方程就是一个系数很小但整数解位数巨大的骇人案例。它不仅仅是令人生畏的符号,而是一项意义深远的研究。
希尔伯特第十大问题的否证陈述意味着,随着系数逐渐增大,解的增长将变为一个不可计算的方程——因为如果它是可计算的,那我们就能得到一个解开丢番图方程的简单算法,而事实上并没有,无论是简单的还是复杂的。
这项研究展现了与那个问题的某种4->80位,178->数亿位,896->数万亿位,让我们瞥见那个怪异的、不可计算的函数的一貌。稍稍把我们的方程改动一下,解就会迅速增长到盖过我们这个“可怜的”、“渺小的”宇宙的任何事物。
何其美妙、何其揶揄的小小方程!
“超级数学建模”(微信号supermodeling),每天学一点小知识,轻松了解各种思维,做个好玩的理性派。60万数学精英都在关注!
,