
利用等底三角形或等底平行四边形的一些性质,进行面积与对应边线段之间的比例相互转化,有助于我们解决一些三角形或平行四边形中的面积问题.
★性质1:如果两个三角形的底相同(或相等),那么它们的面积比等于它们对应的高之比。
☞证明:三角形面积=底×高÷2,很容易得出来:当底相同(或相等)时,面积之比就等于对应的高之比。
☞应用
例1(简单)
已知三角形ABC面积为27平方厘米,AD=2CD,求阴影部分面积。
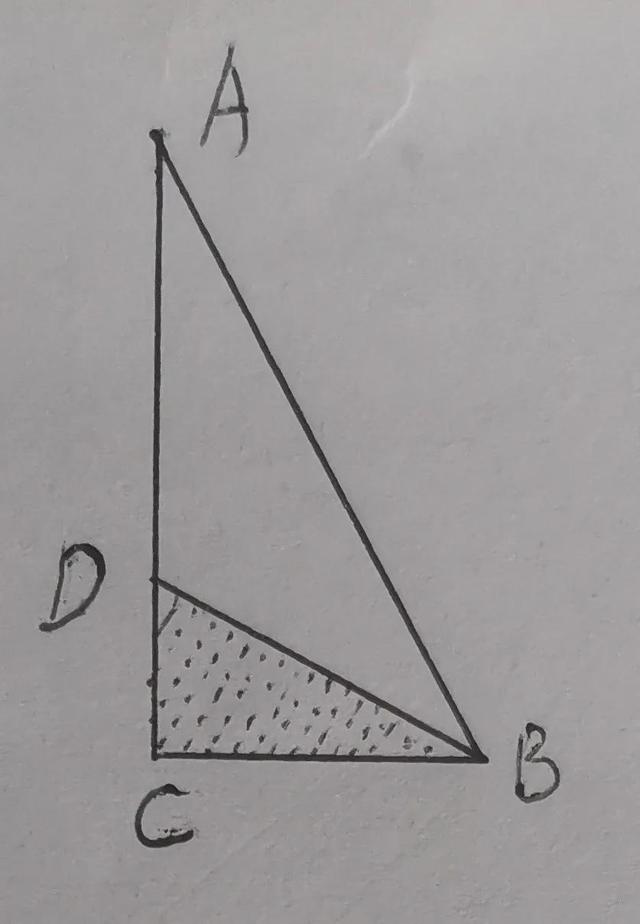
三角形ABC和阴影部分同底,面积之比是高之比(1 2):1=3:1,所以,阴影面积是27÷3=9平方厘米
例2(有难度)
如图所示,有大小两个正方形,求阴影部分面积。

提示:三角形BDC和三角形ABC同底,三角形ADC 面积可求。
★性质2:两个等底三角形面积之和可以合并计算,合并后的高等于二者高之和,底不变。
例3 电子工程师设计了一款机器狗模型,已知CD=DE,FG=2AB ,CB=2AC,三角形ACD面积为9cm²,求阴影部分面积。

提示:图中多个三角形出现了同底现象,可以利用面积之比等于高(组合图形为高的和)之比的性质解题。
练习:在一个长80m、宽40m的长方形麦地中,有一条宽2m的道路从中经过,有下面几种情形(其中阴影部分为道路)。

(1)上面道路占地面积各是多少平方米?你发现了什么?
(2)假设一条小河(河宽总保持2m)恰好从麦地中流过,小河在麦地中占地多少平方米?
答案
(1)根据题干分析可得:40×2=80(平方米)
答:每个图形中的小路的面积都是80平方米,发现规律:在两条平行线间画出平行四边形,无论画出的平行四边形分成几个部分,只有平行四边形的宽不变(等底),它们的高的和不变,则它们的总面积就不变.
(2)40×2=80(平方米),
答:小河在麦地中占地面积是80平方米。
,




