也叫导函数值。又名微商,是微积分中的重要基础概念。当函数y=f(x)的自变量x在一点x0上产生一个增量Δx时,函数输出值的增量Δy与自变量增量Δx的比值在Δx趋于0时的极限a如果存在,a即为在x0处的导数,记作f'(x0)或df(x0)/dx。
导数是函数的局部性质。一个函数在某一点的导数描述了这个函数在这一点附近的变化率。如果函数的自变量和取值都是实数的话,函数在某一点的导数就是该函数所代表的曲线在这一点上的切线斜率。导数的本质是通过极限的概念对函数进行局部的线性逼近。例如在运动学中,物体的位移对于时间的导数就是物体的瞬时速度。
不是所有的函数都有导数,一个函数也不一定在所有的点上都有导数。若某函数在某一点导数存在,则称其在这一点可导,否则称为不可导。然而,可导的函数一定连续;不连续的函数一定不可导。
对于可导的函数f(x),x↦f'(x)也是一个函数,称作f(x)的导函数(简称导数)。寻找已知的函数在某点的导数或其导函数的过程称为求导。实质上,求导就是一个求极限的过程,导数的四则运算法则也来源于极限的四则运算法则。反之,已知导函数也可以倒过来求原来的函数,即不定积分。微积分基本定理说明了求原函数与积分是等价的。求导和积分是一对互逆的操作,它们都是微积分学中最为基础的概念。

偏导数(Partial derivative)原文链接:
https://baike.baidu.com/item/导数/579188
在数学中,一个多变量的函数的偏导数,就是它关于其中一个变量的导数而保持其他变量恒定(相对于全导数,在其中所有变量都允许变化)。
在一元函数中,导数就是函数的变化率。对于二元函数研究它的“变化率”,由于自变量多了一个,情况就要复杂的多。
在 xy 平面内,当动点由 P(x0,y0) 沿不同方向变化时,函数 f(x,y) 的变化快慢一般来说是不同的,因此就需要研究 f(x,y) 在 (x0,y0) 点处沿不同方向的变化率。
在这里我们只学习函数 f(x,y) 沿着平行于 x 轴和平行于 y 轴两个特殊方位变动时,f(x,y) 的变化率。
偏导数的表示符号为:∂。
偏导数反映的是函数沿坐标轴正方向的变化率。

积分(Integral)原文链接:
https://baike.baidu.com/item/偏导数
积分是微积分学与数学分析里的一个核心概念。通常分为定积分和不定积分两种。直观地说,对于一个给定的正实值函数,在一个实数区间上的定积分可以理解为在坐标平面上,由曲线、直线以及轴围成的曲边梯形的面积值(一种确定的实数值)。
积分的一个严格的数学定义由波恩哈德·黎曼给出(参见条目“黎曼积分”)。黎曼的定义运用了极限的概念,把曲边梯形设想为一系列矩形组合的极限。从十九世纪起,更高级的积分定义逐渐出现,有了对各种积分域上的各种类型的函数的积分。比如说,路径积分是多元函数的积分,积分的区间不再是一条线段(区间[a,b]),而是一条平面上或空间中的曲线段;在面积积分中,曲线被三维空间中的一个曲面代替。对微分形式的积分是微分几何中的基本概念。

原文链接:
https://baike.baidu.com/item/积分/5749068
矩阵和向量
矩阵是由m×n个数组成的一个m行n列的矩形表格.特别地,一个m×1矩阵也称为一个m维列向量;而一个1×n矩阵 ,也称为一个n维行向量。
依上定义可以看出:向量可以用矩阵表示,且有时特殊矩阵就是向量。
简言之就是矩阵包含向量。
对角矩阵对角矩阵(diagonal matrix)是一个主对角线之外的元素皆为0的矩阵,常写为diag(a1,a2,...,an) 。对角矩阵可以认为是矩阵中最简单的一种,值得一提的是:对角线上的元素可以为 0 或其他值,对角线上元素相等的对角矩阵称为数量矩阵;对角线上元素全为1的对角矩阵称为单位矩阵。对角矩阵的运算包括和、差运算、数乘运算、同阶对角阵的乘积运算,且结果仍为对角阵。
同阶对角矩阵的乘积仍为对角阵,且它们的乘积是可交换的。

原文链接:
https://baike.baidu.com/item/对角矩阵
鞍点(Saddle point)
长期以来,人们普遍认为,神经网络优化问题困难是因为较大的神经网络中包含很多局部极小值(local minima),使得算法容易陷入到其中某些点。到2014年,一篇论文《Identifying and attacking the saddle point problem in high-dimensional non-convex optimization》,提出高维非凸优化问题之所以困难,是因为存在大量的鞍点而不是局部极值(Local optima)。
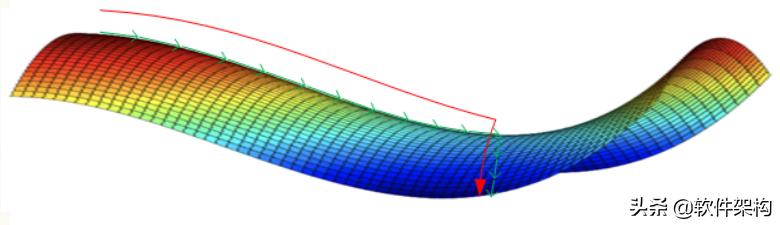
鞍点:一个维度向上倾斜且另一维度向下倾斜的点。这些鞍点通常被相同误差值的平面所包围,这使得算法陷入其中很难脱离出来,因为梯度在所有维度上接近于零。
图一表示:神经网络只有两个参数时的情况(水平方向分别为两个参数,纵轴代表损失函数),有多个局部最小值
图二表示:神经网络具有高维参数时,可看到有鞍点。

鞍点(saddle point) 这个词来自z=x^2−y^2 的图形,在x轴方向向上曲,在y轴方向向下曲,像马鞍,鞍点为(0,0)。

拥有两个以上参数的函数。它的曲面在鞍点好像一个马鞍,在某些方向往上曲,在其他方向往下曲。
神经网络优化问题中的鞍点
神经网络优化问题中的鞍点即一个维度向上倾斜且另一维度向下倾斜的点。
在鞍点附近,基于梯度的优化算法(几乎目前所有的实际使用的优化算法都是基于梯度的)会遇到较为严重的问题:
鞍点处的梯度为零,鞍点通常被相同误差值的平面所包围(这个平面又叫Plateaus,Plateaus是梯度接近于零的平缓区域,会降低神经网络学习速度),在高维的情形,这个鞍点附近的平坦区域范围可能非常大,这使得SGD(Stochastic Gradient Descent,随机梯度下降法)算法很难脱离区域,即可能会长时间卡在该点附近(因为梯度在所有维度上接近于零)。
在鞍点数目极大的时候,这个问题会变得非常严重。
高维非凸优化问题之所以困难,是因为高维参数空间存在大量的鞍点。
原文链接:
https://blog.csdn.net/baidu_27643275/article/details/79250537
正弦和余弦
在直角三角形中,∠α(不是直角)的对边与斜边的比叫做∠α的正弦,记作sinα,即sinα=∠α的对边/∠α的斜边 。
正弦是∠α(非直角)的对边与斜边的比,余弦是∠α(非直角)的邻边与斜边的比。
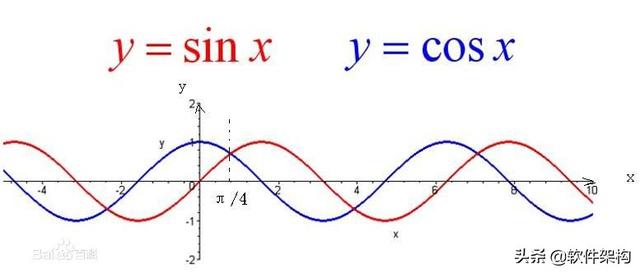
正弦的最大值为1,最小值为-1。
另外,当sin值在180~360之间会出现负数,在360以上则会重复。

原文链接:
https://baike.baidu.com/item/sin/391892
希腊字母
Delta是第四个希腊字母的读音,其大写为Δ,小写为δ。
在数学或者物理学中大写的Δ用来表示增量符号。 而小写δ通常在高等数学中用于表示变量或者符号。
希腊字母表的第十八字母(∑,σ)。∑ 英语名称:Sigma 汉语名称:西格玛(大写Σ,小写σ)。
,




