今天我们用scratch的小程序来判定质数。

判定质数提问
判定质数1
判定质数2
题目:给你一个大于1的自然数,请判断它是合数还是质数。
角色:小猫;
知识点:质数,循环,选择,侦测,变量;
质数知识普及:
概念:质数就是只有1和它自身两个因数的数。
判定质数的方法:
1)直观判断法:根据定义,直接判断从2到n-1是否存在n的约数,就是看n能不能被2到n-1中的某个数整除。只要有一个数能被n整除,n就是合数;如果都不能被n整除,n就是质数。比如79,我们就看它能不能被2到78中的某一个数整除。
2)算术平方根判断法:上述判断方法,明显存在效率极低的问题。对于每个数n,其实并不需要从2判断到n-1,我们知道,一个数若可以进行因数分解,那么分解时得到的两个数一定是一个小于等于sqrt(n),一个大于等于sqrt(n),据此,上述代码中并不需要遍历到n-1,遍历到sqrt(n)即可,因为若sqrt(n)左侧找不到约数,那么右侧也一定找不到约数。
一、准备工作
1、背景和角色:今天的小程序背景和角色都使用系统默认的;
2、变量:新建两个变量,分别命名为“n”和“i”,变量n存储需要判定的数,变量i作为循环变量;

变量i
二、编辑脚本
1、初始化,变量赋值:两个变量初始化为0,侦测到输入的数后,给变量n赋值“回答”,变量i赋值2,表示从2开始试除;

变量初始化赋值
2、循环条件:当循环变量i大于变量n的算术平方根时,退出循环,说明没有可以整除变量n的数,当前的数n为质数;

循环条件
3、选择判断1:循环体内部使用有两个分支的选择结构,“如果……那么……否则……”,如果从2开始有可以整除n的数,即n/i余数为0,那么变量n就是合数,停止全部脚本;

选择判断1
4、选择判断2:否则,从2开始到n的算术平方根,逐一判断如果不能整除n,即n/i余数不为0,那么给变量i增加1,继续循环;
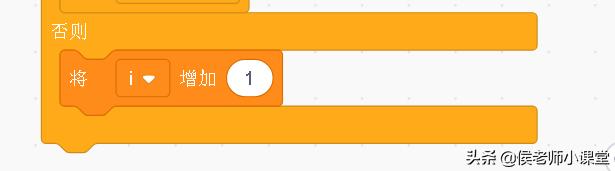
选择判断2
三、完整脚本
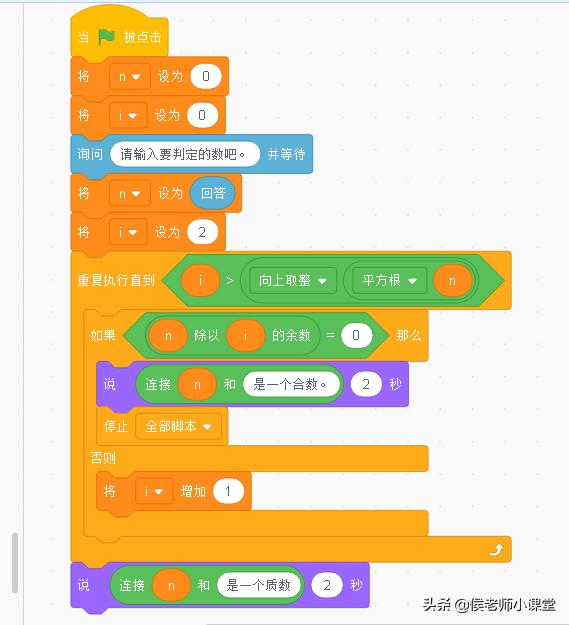
完整脚本
想一想,如果想使用直观判断法的话,怎么修改脚本呢?
,




