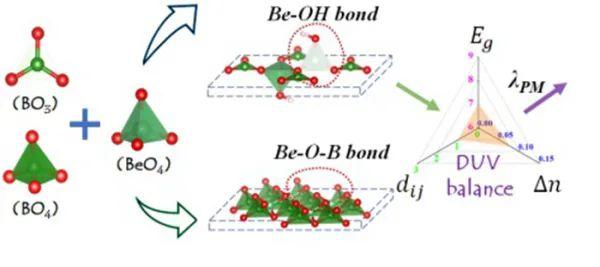
5月5日立夏,跟朋友们聊起了立夏的习俗,比如说:祭祖祭神、挂蛋。此外还有一个非常特别的习俗——称体重。·据说,立夏这一天称了体重之后,就不怕夏季炎热,人也不会消瘦,如果不称体重就会有病灾缠身。
古人称重用的工具是一杆大木称,秤钩悬一根凳子,大家轮流坐到凳子上面秤人。其实这种称与中药铺中用的小称盘的原理是一样的——杠杆原理。阿基米德曾经有一个经典名言:“给我一个支点和一根足够长的杠抄杆,我就可以撬动地球”。

看上去用杠杆原理称地球的重量应该是可行的,但事实上做不到。因为我们既找不到那么长和坚固的秤杆,也找不到悬挂秤杆的支点。到底怎么才能称出地球的体重呢?(重量和质量不是同一个物理量,严格说,应该是称量地球的质量。)
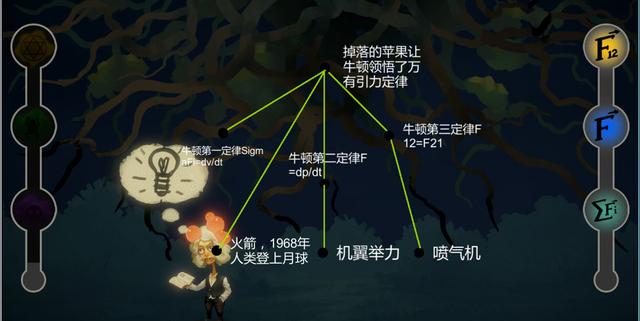
这个问题直到牛顿发现了万有引力定律的时候才有了解决的方法。估计万有引力这个公式F=GMm/r^2,大家也都没忘记。咱们一起来看看是怎么从这个公式中找到跟给地球称“重”的方法的。
从这个公式其实可以找出两种给地球称“重”的方法:

这种方法是在牛顿想到的第一个办法。因为,虽然当时牛顿得到了万有引力的公式,但公式中那个万有引力常数G的值是多少牛顿自己也不知道。
按说只要测出两个物体的质量,物体质心间的距离,再测出两个物体之间引力的大小,代入前面那个万有引力公式,就能计算出这个常数。无奈,普通物体的质量都太小了,我们无法测出它们之间的引力。而天体的质量又太大了,也不能直接测出质量。这也导致了,牛顿提出万有引力公式之后100年内,这个常数都没人能测出一个准确值来。
牛顿是怎么从公式里面找到单摆法的呢?其实牛顿公式中暗含着地球对它吸引的物体施加的加速度g与万有引力常数之间的关系,即,g=GM/r^2。但这个g是一个局部的量,地球上不同地方g的值会有一个微小的差异。但这不要紧,这个方法总是可以得到一个比较接近的数值。具体操作方法是下面这样的:
做一个单摆,这个简单,就是用一根细线挂一个重物,摆锤会在重力的作用下,处于一个稳定状态,也就是说稳定在那个平衡点上。当然了,事实上这做不到,做过物理实验的小伙伴都明白这一点。不过这不要紧,即使单摆摆动起来也不要紧,因为只要单摆处于摆动平衡状态也是可以的。
这样一个单摆,实际上就是形成了地球和单摆的一个系统。如果我们此时在单摆的旁边放一个已知质量和形状的物体,会发生什么呢?单摆会被这个大物体吸引,从而导致摆动的角度(平衡点的位置)发生变化,即向着这个大物体方向发生偏转。只要这个物体质量非常大,那么单摆偏离原来平衡位置的角度就能被观测出来。
现在就形成了地球、单摆、大质量物体共同组成的一个系统。单摆偏转的角度值(弧度)就是大质量物体对重锤的引力与地球引力的比值。即θ=M1R^2/M2r^2,其中M1是额外加进来的那个大质量物体、R是地球半径、M2是地球质量、r是重锤质心与M1质心之间的距离、θ是单摆偏离平衡位置的角度。

那么去哪找这么一个已知形状的大质量物体呢?科学家们能想到的是“山”。好吧,这脑洞是真够大的,但真的有人去这么干了。一帮科学家们在伦敦郊外找了一个大山,对山体进行了测量,并且支起了一个巨大的支架,做了一个单摆。
说真的,光是联想那些科学家用这个方法测量地球质量的画面,我就已经在风中凌乱了。具体的是不是测量出结果了,我没有查到资料,就不多说了。这种办法与狂人阿基米德的豪言相比,很明显——靠谱。
如果我们认真分析这个比较法,其实试验中得到的直接测量结果是单摆的偏转角度,而影响实验测量精度的最大因素是那个山的密度的测量。偏转角度也可以换算成地球密度与山体密度的比值。后来这个单摆实验得到了改进,但其测量目的其实没变——也是为了得到地球的密度。这就是我们下面要介绍的——卡文迪许扭摆实验。

这个扭摆实验实在是太有名了,同样出现在我们的高中课本里,即使科技迅猛发展到了今天,地球上测量万有引力常数最领先的华中科技大学团队,依然使用的是这种方法。
虽然这套扭摆装置被称作卡文迪许扭摆,但其实这套装置的发明人是英国皇家学会的米歇尔神父。米歇尔制作扭秤的目的与最早尝试测量地球质量的人一样是为了测定地球的密度,并与卡文迪许讨论过这一问题。但是,米歇尔还未用它来进行测定,便去世了。
米歇尔去世后,这架仪器几经辗转传到了剑桥大学教授沃莱斯顿神父手里,他又慷慨地赠送给了卡文迪许,这时卡文迪许已是年近古稀的老人了。
卡文迪许首先根据自己实验的需要对米歇尔制作的扭秤进行的分析,他认为有些部件没有达到他所希望的方便程度,为此,卡文迪许重新制作了绝大部分部件,并对原装置进行了一些改动。

卡文迪许认为大铅球对小铅球的引力是极其微小的,任何一个极小的干扰力就会使实验失败。他发现最难以防止的干扰力来自冷热变化和空气的流动。为了减小误差,卡文迪许把整个装置放在一个封闭的房间里,通过望远镜从室外观察扭摆臂杆的移动。
扭摆的主要部分是一个轻而坚固的T形架,倒挂在一根金属丝的下端。T形架水平部分的的两端各装一个质量是m的小球,T形架的竖直部分装一面小平面镜M,它能把射来的光线反射到刻度尺上,这样就能比较精确地测量金属丝的扭转。
实验时,把两个质量都是m'的大球放在如图所示的位置,它们跟小球的距离相等。由于m受到m'的吸引,T形架受到力矩作用而转动,使金属丝发生扭转,产生相反的扭转力矩,阻碍T形架转动。当这两个力矩平衡时,T形架停下来不动。

这时金属丝扭转的角度可以从小镜M反射的光点在刻度尺上移动的距离求出,再根据金属丝的扭转力矩跟扭转角度的关系,就可以算出这时的扭转力矩,进而求得m与m'的引力F。这个万有引力是非常小的,实际生活中几乎不可能感受到,但是确实存在。
卡文迪许是利用小球的与地球的比例关系来测量出的地球质量,从而得出地球平均密度(这也是卡文迪许生前最后的一项研究)约为5.448克/厘米,现在公认的是5.507克/厘米,已经相差无几。卡文迪许通过他的实验估计出地球的质量大概是60万亿亿吨,和现有的公认值5.972 10^24 kg很接近。
如果我们利用卡文迪许的数据进行进一步的推算是可以得到万有引力常数G的值的。一般性地说在天文单位上,G是地球密度的倒数,卡文迪许测到了地球密度,自然也算得到G了。

测量地球质量这个事太重要了,只要知道了地球的精确质量,就能知道太阳质量是多少,进而计算出其他天体的质量。在人类称量地球的过程中,卡文迪许扭摆是目前最有效的方法,没有之一。
我们从寻找给地球称重办法的历史故事中应该了解物理学的另外一个分支——实验物理。它向我们展示的是物理学的另一种魅力,物理学不仅有理论,更有实验。无实验不物理,这个理念您Get到了吗?
不知道小伙伴们是不是通过这篇文章对万有引力定律有了更深的了解呢?欢迎您在下方留下您的宝贵意见。
,