杨辉,字谦光,钱塘(今浙江省杭州)人,南宋时期杰出的数学家、数学教育家,他曾担任过南宋地方行政官员,为政清廉,足迹遍及苏杭一带。他在总结民间乘除捷算法、“垛积术”、纵横图以及数学教育方面,均做出了重大的贡献。他是世界上第一个排出丰富的纵横图和讨论其构成规律的数学家。还曾论证过弧矢公式,时人称为“辉术”。 他与秦九韶、李冶、朱世杰并称“宋元数学四大家”。
杨辉对各种数阵的研究怀有特别浓厚的兴趣,他是最早系统研究幻方的数学家。n阶幻方是指由前n^2(n的2次方)个自然数组成的一个n阶方阵,其各行、各列及两条对角线所含的n个数的和相等。比如像下面这样其各行、各列及两条对角线所含的数的和都为15的图,我国古代把它叫做纵横图或九宫格,国外把它叫做三阶幻方。

九宫格
事实上,南北朝的甄鸾在《数术记遗》一书中就研究过九宫格的填法:“九宫者,二四为肩,六八为足,左三右七,戴九履一,五居中央。”而在杨辉的《续古摘奇算法》中,他进一步总结出了三阶幻方构造的方法:九子斜排,上下对易,左右相更,四维挺出”。就是说:一开始将九个数字从大到小斜排三行,然后将9和1对换,左边7和右边3对换,最后将位于四角的4、2、6、8分别向外移动,排成纵横三行,就构成了九宫图。按照类似的规律,杨辉又得到了“花16图”,就是从1到16的数字排列在四行四列的方格中,使每一横行、纵行、斜行四数之和均为34。后来,杨辉又将散见于前人著作和流传于民间的有关这类问题加以整理,得到了“五五图”、“六六图”、“衍数图”、“易数图”、“九九图”、“百子图”等许多类似的图。这些成果都被收录在他的数学著作《续古摘奇算法》一书中,并流传后世。
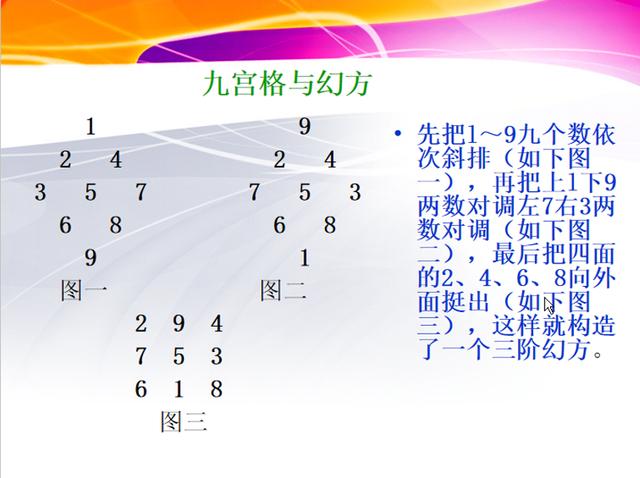
杨辉填九宫格方法
除了幻方之外,杨辉最广为人知的重大贡献就是“杨辉三角”的发现。有一次,杨辉得到一本《黄帝九章算法细草》,这是北宋数家贾宪写的。这里面有不少了不起的成就,如贾宪描画了一张图,叫作“开方作法本源图”。图中的数字排列成一个大三角形,位于两腰上的数字均是1,其余数字则等于它上面两数字之和。从第二行开始,这个大三角形的每行数字,都对应于一组二项展开式的系数,下面试举例说明:在第三行中,1、3、3、1,这4个数字恰好是对应于(X 1)3=X3 3X2 3X 1;再如第四行对应于(X 1)4=X4 4X3 6X2 4X 1。以此类推。杨辉把贾宪的这张画忠实地记录下来,并保存在自己的《详解九章算术》一书中。这就是“杨辉三角”,在西方也叫“帕斯卡三角”。帕斯卡(1623----1662)是在1654年发现这一规律的,比杨辉要迟393年,比贾宪迟600年。杨辉三角是中国古代数学的杰出研究成果之一,它把二项式系数图形化,把组合数内在的一些代数性质直观地从图形中体现出来,是一种离散型的数与形的结合。

杨辉三角
“杨辉三角”有不少有趣的性质。首先,(a b)n的展开式中的各项系数依次对应杨辉三角的第(n 1)行中的每一项。其次,从第2行起,每一行的第二个数(或倒数第二个数)依次是1,2,3,4……。再比如,每个数字等于上一行的左右两个数字之和,比如第6行第3个数10=4 6,正好是10的上一行左右两数之和,可用此性质写出整个杨辉三角。还有,第n行各数之和正好为2的n-1次方。此外,杨辉三角还与组合数、斐波拉契数列有密切的联系,这里就不赘述了。
杨辉著名的数学书共五种二十一卷。著有《详解九章算法》十二卷(1261年)、《日用算法》二卷(1262年)、《乘除通变本末》三卷(1274年)、《田亩比类乘除算法》二卷(1275年)、《续古摘奇算法》二卷(1275年)(后三种合称为《杨辉算法》)。
杨辉所著的《详解九章算法》从残本的体例看,对《九章算术》的详解可分为:一、解题。内容为解释名词术语、题目含义、文字校勘以及对题目的评论等方面。二、明法、草。在编排上,杨辉采用大字将贾宪的法、草与自己的详解明确区分出来。三、比类。选取与《九章算术》中题目算法相同或类似的问题作对照分析。四、续释注。在前人基础上,对《九章算术》中的80问进一步作注释。杨辉的“纂类”,突破《九章算术》的分类格局,按照解法的性质,重新将《九章算术》246个题目分为乘除、分率、合率、互换、衰分、叠积、盈不足、方程、勾股九类。
他在《续古摘奇算法》中介绍了各种形式的"纵横图"及有关的构造方法,同时"垛积术"是杨辉继沈括"隙积术"后,关于高阶等差级数求和的研究。
杨辉不仅是一位著述甚丰的数学家,而且还是一位杰出的教育家。他一生致力于数学教育和数学普及,其著述有很多是为了数学教育和普及而写。杨辉的数学研究与教育工作的重点是在计算技术方面,他对筹算乘除捷算法进行总结和发展,有的还编成了歌决,如九归口决。《算法通变本末》中载有杨辉专门为初学者制订的“习算纲目”,它集中体现了杨辉的数学教育思想和方法。
总而言之,杨辉的几部著作极大地丰富了我国古代数学宝库,为数学科学的发展做出了卓越的贡献,他不愧为“宋元四大家”之一。
,