机器学习回归数学原理（机器学习中的线性代数）

（一）前言

1、总结大数据、人工智能机器学习中的数学知识

2、已经调试通过直接运用，减少查找资料的时间

3、您的关注就是对我对大的支持，也是对科技的支持

机器学习的核心技术是以数学和数据结构算法为主的基础学科，包括高等数学、线性代数、数论、图论、决策论等等基础理论知识点，在实际的工程实践中出现了很多数学工具比如R语言数学库，商用MATLAB数学库，近年来Python数学库发展的很快，这里涉及到的案例将使用Python语言描述，为了方便大家的运用，本篇文章将线性代数常用的知识点总结出来，可以方便大家的引用，也可以作为大学生和大学教师的参考课件。

本篇文章涉及到的案例基本都是笔者亲自调试通过，要求Python3.6以上版本，要安装numpy、pandas、sklearn、 matplotlib等常见类库，特别说明不建议读者使用Python2.7版本。建议大家使用Pycharm来提高效率。

（二）矩阵

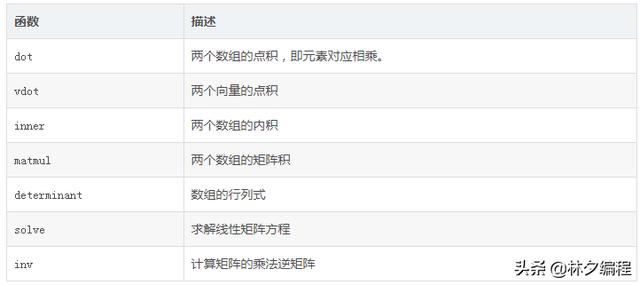
矩阵的运算有加减乘、求矩阵的逆、求矩阵的秩、矩阵的转置等运算，矩阵的运算在线性回归中有着重要的作用，数据分析领域也起着重要的作用，比如关系型数据库本质就是矩阵的各种运算。

1、矩阵的加法

import numpy as npa1 = np.array([[1,2,3]])a2 = np.array([[4,5,6]])print(a1 a2 )

2、矩阵的乘法

设有两个矩阵A和B，A为3x2矩阵，B为2x3矩阵，乘积的结果为C3x3矩阵，矩阵乘积的规则大家都学过了，再温习下，如下图所示：

机器学习回归数学原理（机器学习中的线性代数）(1)

import numpy as npA = np.array([[1,2],[3,4],[5,6]])B = np.array([[1,2,3],[4,5,6]])print(np.dot(A,B) )

A x B = C ，结果为：

[[ 9 12 15]

[19 26 33]

[29 40 51]]

C 的第1行为：1x1 1x4 1x2 2x5 1x3 2x6

C 的第2行为：3x1 4x4 3x2 4x5 3x3 4x6

C 的第3行为：5x1 6x4 5x2 6x5 5x3 6x6

3、求矩阵的秩

矩阵A的列秩是A的线性独立的纵列的极大数目。类似地，行秩是A的线性无关的横行的极大数目。如果把矩阵看成一个个行向量或者列向量，秩就是这些行向量或者列向量的秩，也就是极大无关组中所含向量的个数。

import numpy as npfrom scipy import linalgA = np.array([[1, 0, 0], [0, 1, 0], [0, 0, 1], [0, 0, 0]])#非0的行数就是矩阵的秩n = np.linalg.matrix_rank(A)print(n)

结果：n = 3

4、求矩阵的逆

设A是数域上的一个n阶方阵，若在相同数域上存在另一个n阶矩阵B，使得: AB=BA=E。则我们称B是A的逆矩阵，而A则被称为可逆矩阵。

import numpy as npfrom scipy import linalgA = np.array([[1, 2 ], [3, 4, ] ])An = linalg.inv(A)print(An)

5、求解线性方程组

有个方程组如下所示：

X1 x2 x3 = 10

X1 - x2 x3 = 6

X1 - x2 - x3 = 0

import numpy as npfrom scipy import linalgA = np.array([[1, 1, 1], [1, -1, 1], [1, -1, -1]])y = np.array([10, 6, 0])x = linalg.solve(A, y)print(x)

结果：[5. 2. 3.]

（三）向量

1、向量的概念

在线性代数中的向量是指n个实数/复数组成的有序数组，称为n维向量。α=（a1，a2，…，an）称为n维向量。其中ai称为向量α的第i个分量。

2、行向量和列向量

（1）行向量

import numpy as npV = np.array([1,2,3 ])print(V)

（2）列向量

import numpy as np#行向量v1 =np.array([[1,2,3]])#v1转置v2 = v1.Tprint(v2 )

3、向量的运算

（1）向量的加法

import numpy as npv1 = np.array([[1,2,3]])v2 = np.array([[4,5,6]])print(v1 v2 )