高中数学立体几何章节检测题
一、填空题:
1、A,B,C为空间三点 , 经过这三点的平面有 _______ 个。
2、两个球的半径之比为1∶2,那么两个球的表面积之比为________。
3、已知 a,b 是两条异面直线,直线 c 平行于直线 a,那么直线 c 与直线 b 的位置关系是____________。
4、 空间中直线 l 和三角形的两边AC,BC同时垂直,则这条直线和三角形的第三边AB的位置关系是________。
5、以下角:①异面直线所成角;②直线和平面所成角;③二面角的平面角,可能为钝角的有________个。
6、过平面外一点能作 _______ 条直线与这个平面平行。
7、已知一个正方体的所有顶点在一个球面上.若球的体积为 9π/16 ,则正方体的棱长为________。
8、如图所示的水平放置的平面图形的直观图,它所表示的平面图形ABCD是 ________。

第8题图
9、如图所示,P是三角形ABC所在平面外一点,平面α∥平面ABC,α分别交线段PA、PB、PC于A′、B′、C′,若PA′∶AA′=3∶4,
则S△A′B′C′∶S△ABC=________。
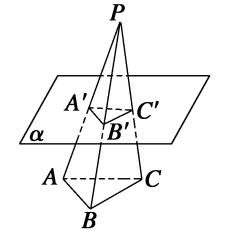
第9题图
10、已知平面 α 外两点 A、B到平面 α 的距离分别是3和5,则A,B的中点P到平面α的距离是________。
11、若圆锥的全面积是底面积的3倍,则该圆锥的侧面展开图扇形的圆心角为________度。
12、如图,已知高为3的棱柱ABC—A1B1C1的底面是边长为2的正三角形,则三棱锥B1—ABC的体积为________。

第12题图
13、 在正四面体P-ABC中,D、E、F分别是AB、BC、CA的中点,下面四个结论中不成立的是________。
①BC∥面PDF;②面PDF⊥面ABC;③DF⊥面PAE;④面PAE⊥面ABC。

第13题图
14. 设α∥β,A∈α,C∈α,B∈β,D∈β,直线AB与CD交于O,若AO=8,BO=9,CD=51,则CO=________。
二、解答题
15、已知:平面α∩平面β=b,直线a∥α,a∥β,求证:a∥b。

第15题图
16、已知ABCD是空间四边形,AB=AD,CB=CD ,求证:AC⊥BD 。

第16题图
17、 如图所示,P是四边形ABCD所在平面外的一点,四边形ABCD是∠DAB=60°且边长为a的菱形.侧面PAD为正三角形,其所在平面垂直于底面ABCD。
(1) 若G为AD边的中点,求证:BG⊥平面PAD;(2) 求证:AD⊥PB。

第17题图
18、如图,在三棱锥 P-ABC 中,平面 PAB ⊥平面 PBC ,AB⊥BC,AP=AB,过 A 作 AF⊥PB 垂足为 F,点 E , G 分别是棱 PA ,
PC 的中点。
求证:(1)平面 EFG∥平面 ABC ; (2)BC⊥PA 。

第18题图
19、已知正方体 ABCD-A1B1C1D1 的棱长为1,P、Q 分别是正方形 AA1D1D 和 A1B1C1D1 的中心。
(1)证明:PQ∥平面DD1C1C;(2)求线段PQ的长;(3)求PQ与平面AA1D1D所成的角 。

第19题图
20、如图,在四面体ABCD中,CB=CD,AD⊥BD,且E、F分别是AB、BD的中点。
求证:(1)EF∥面ACD; (2) 面EFC⊥面BCD。

第20题图
高中数学立体几何章节检测题
参考答案
一、 填空题:
① 1或无数个 ② 1∶4 ③ 相交或异面 ④ 垂直 ⑤ 1 ⑥ 无数条 ⑦ √3/2 ⑧ 直角梯形 ⑨ 9∶49 ⑩ 4或1
⑪ 180 ⑫ √3 ⑬ ② ⑭ 24或408
二、解答题
15、证明:

16、证明:

17、证明:
(1) 连结PG,由题知△PAD为正三角形,G是AD的中点, ∴PG⊥AD。
又平面PAD⊥平面ABCD, ∴PG⊥平面ABCD, ∴PG⊥BG。
又∵四边形ABCD是菱形且∠DAB=60°, ∴BG⊥AD。
又AD∩PG=G,∴BG⊥平面PAD。
(2) 由(1)可知BG⊥AD,PG⊥AD。
所以AD⊥平面PBG,所以AD⊥PB。
18、证明:


19、证明:

20、证明:
(1) ∵ E,F分别是AB,BD的中点,
∴ EF是△ABD的中位线,∴EF∥AD,
∵ EF⊄面ACD,AD⊂面ACD,∴ EF∥面ACD。
(2) ∵ AD⊥BD,EF∥AD,∴ EF⊥BD。
∵ CB=CD,F是BD的中点,∴ CF⊥BD。
又 EF∩CF=F,∴ BD⊥面EFC.∵ BD⊂面BCD,
∴ 面EFC⊥面BCD。
,




