卡尔曼滤波是贝叶斯滤波的一种特例,是在线性滤波的前提下,以最小均方误差为最佳准则的。估计线性高斯模型,是对线性模型和高斯分布的优化方法。
高斯分布首先,回顾一下高斯分布:

高斯分布的一些性质:
如果原变量为高斯分布,则边缘化和条件概率仍然满足高斯分布。

边缘分布和条件分布的模型:

卡尔曼滤波器假设x(paths), z(observations)都为线性高斯的:

主要参数:

A是在没有命令的情况下,由于环境因素造成的机器人的位置移动。
B是命令对机器人位置的改变
C是地图和observations的对应关系,即两者的联系,描述。
最后两个为噪声,是由于测量中的误差造成的。协方差分布为R, Q。
线性motion model和observation model
因为之前已经假设了x,z都是高斯分布的
运动模型:

观测模型:

由此就可以使用第三节的贝叶斯滤波器公式:


2,3是prediction过程,4-7是correction过程。
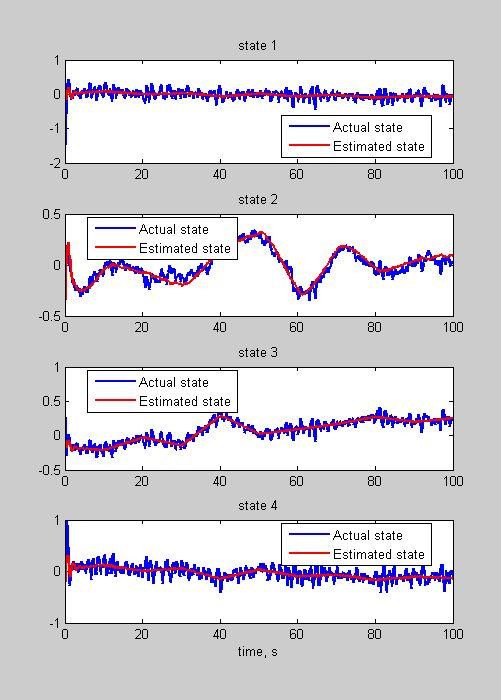
其实卡尔曼滤波就是在估计和测量中找到一个平衡。
K为卡尔曼增益,就是通过这个变量来调节估计和预测的平衡。

卡尔曼滤波是在假设高斯和线性动作和观测模型下进行的,但是现实中并不是这样的。
What’s Extended Kalman Filter
引入非线性模型:

在线性高斯模型中:

在非线性高斯模型中:

通过局部线性来解决非线性的问题。
复习Jacobian矩阵

它相当于对一个非线性函数做了切平面。


用图表示为:


由此运动模型和观测模型修改为: