
三角函数题型,作为我们高中题型的重点题型,也是目前现在高考考查一个非常重要的内容,而对于三角函数值域转换题型,很多同学并不非常理解。一遇到这种题型,经常会出现思路断片,或者不懂得如何入手,经常解答方法错误,解答繁琐,易题难解。
在这里我跟大家分享这一类三角函数值域转换题型,全面分析一下,这样有助于同学们在更加有效的理解这一类三角函数值域转换题型,可以更好的去驾驭这一类三角函数值域转换题型。


前期工作,如果遇到这种三角函数值域转换题型,首先大家一定要回归到我们的正弦函数,余弦函数的最基础图像,一定要把这个原始图像熟悉,熟悉再熟悉。
因为三角函数其实并无难题,所有的三角函数,由于这个图像限制,所以它所有的题目必须按照这个原始图像出发,在完成这类三角函数值域转换题型,唯一要求,一定必须把正弦函数,余弦函数这个原始特征全部记好,唯一的一个要求,一定要。



在这里的话,我列举了总共是10道这一个题目,给同学们自行完成。
同学们尝试一下用个人的一些方法,把上述这10道题目全部完成,利用个人所知的各种方法进行分析,与后续我们提供的模板方法进行比较,这也是数学思维养成的重要过程。
因为这个三角函数值域题型,其实可以不变应万变,只要一旦题目提供这个x的范围,那么这样的题目我们就可以统一称三角函数值域题型,但因为题目之间一些细微变化的话,就有时会出现三角函数值域转换题型,这点大家可以自行进行总结归纳。


这个三角函数值域转换题型,通过第1道例子,我们可以发现,这种题型的解题步骤:
一、确定x范围;
二、确定这个整体范围;
三、原图的分析;
四、把原图所知信息都标注;
五、确定这个不等式;
六、分析结果。
以后遇到三角函数值域转换题型,可以按照我们上面这六步曲进行这个分析解答,若与同学们之间这个想法有冲突,希望同学们能够按照这种模板化的思路去进行,因为三角函数自身的图像极度重要,很多同学在三角函数题型分析上,并未考虑原图形的影响,而是按照个人的步骤去进行,这点是非常不理智的。
数学里面所有的题型必须按照概念基础性质进行,每一道题的解决过程中不会按照你的解题方式进行,而是你一定必须把每一个概念都理解好,这样学习效率才能达到最大化。
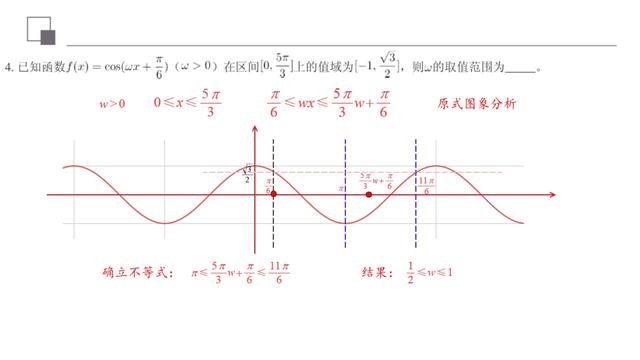
再看第2道例子,发现这种三角函数值域转换题型跟前面六个步骤是一模一样的,再次确定我一定要遇到三角函数值域转换题型,先把前面学习的六步个骤熟记,熟记,按部就班进行,这样能大大提高我们对这种三角函数值域转换题型认知感,对于数学思维养成也是非常有必要的。也就可以更大一方面杜绝这个很多同学犯错问题,看清楚这一类三角函数值域转换题型模式,提高学习效率。


那我们再通过两个例子,把这个思维进行巩固,确保达对这种三角函数值域转换题型的理解,
以保障达到一个非常固定化的模式。
数学解题过程最重要的就是一个思维就是题型化,大量题目解法基本是相同的,这一点的话很多同学很少去意识到,某一种类型它的解法几乎是一致的,但是转换出题方式之后,很多同学就会出现断片、理解错误、思路错误,解法上出现了更大的问题,所以,以上两个例子,把这个思维进行固化,但是题型会转变的,后续的几道题题型,给大家带来更大冲击,这样也能够提高我们对数学题型的一个理解与转化。
异题同类分析

这道例子,出现了这一个x范围是确定的,但与上面例子问题分析有了质的区别。
然后,同学们细心体会这个分析过程,它跟我们前面这个分析题型是一样的,但它问题出现的方式不同,求解过程并不一样。
但它跟我们前面这个分析题型又有类似的地方,就是它x范围已经确定。
所以,以后同学们遇到这种x范围确定,只要x范围确,统一归类,它们都是千篇一律的一种模式,虽然说求解过程不一样,解法基本上没有变化,这一点对很多同学并不理解,只能说明这个三角函数的特点,很多同学在学习归纳上并没有注意好这种题目的特点。
再次强调只要x范围提供,这种题目就一定属于三角函数值域的题目,至于题型转换,随之题目要求不同而转换,而我们只需要做好几个工作:
第1个确定x范围;
第2个确定整体范围;
第3个分析原始图像;
第4个由原始图像去分析我们所需要的内容;
第5个分析情况;
第6个确定结果。
这样就可以达到一个非常有效的解决三角函数,不同题目,不同题型,归纳分析题型的一致性。


为了确保同学们对这种三角函数值域转换题型的一致性,我们这里再提供两道题目,给大家进行分析理解,以确保同学们以后遇到这种三角函数值域转换题型的题目,明白它们之间转换思路,而且确保同学们在遇到这一类题的时候,学会怎么去完成。
那么以上这些题目的分析的话,大家可以重复再看几遍,因为这个点也是三角函数在高考的常考点,也是所有同学们最怕的一个内容。
只要大家能够把这种三角函数值域转换题型通过我们前面讲过的这个6个步骤的解法,以后遇到只要这种x范围确定的题目,可以大胆放心去做,确保所有同学在遇到上这类题型时,明确解法。
三角函数本身就没有难题,题目怎么变,图像永远只有原始图像。这点的话,可能很多同学在这个学习过程中并没有注意到,由于平时大家完成题目过多,会把这个注意力转移,那么我们希望通过这篇文章,大家以后能够确立好这种题型的解法。
后续,大家如果还有其他疑问的话,也可以跟我们这个留言进行交流,我们也希望可以提供更多题型解法分析给大家。






