前面几天的话题我接不下去了,今天转台,写个不是太复杂的内容
说起来,线性回归这个东西我之前是写过的,而且仔细算算的话恐怕还不止一次,但是到今天再回过头去翻翻自己当时(大概两个月前)写的东西,感觉自己之前学的也好,用的也好,都还挺浅的——即使现在也深不到哪儿去

我特意去翻出了两个月前头回写线性回归时编的那个例子:

答案我也先放出来,以便后面检查:

当时还挺自以为是的用了几种不同的方式来做,但今天不啰嗦那么多,就只补充一种比较骚气的计算方法——用数组和向量来计算线性回归公式里的系数(a和b)
公式就一个,是从书上来的:
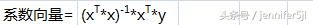
上标T表示矩阵行列转置,对应Excel公式TRANSPOSE(行列位置交换)
上标-1表示矩阵求逆,对应Excel公式MINVERSE
请注意一个特殊的地方,由于整个公式是矩阵/向量级别的计算,所以里面的乘号不是指一般的乘法,而是矩阵乘法公式MMULT,而且,更更更关键的部分是,矩阵乘法是不支持交换律的(也就是AxB不等于BxA),所以,计算乘法的顺序从左到右一点都不能乱了——否则就会像我一样公式打错一卡住就半个多小时T-T
开始之前,还有点准备工作要做,那就是去平均值(x列y列各自减掉它们的平均值)

为什么咧?因为书上用的这个公式是基于一个假设推导出来的,这个假设为:
y向量= 系数向量T * x向量
发觉没,这里面没有常数项b,也可以说,它假设了b=0,解释得再完整点,就是假设拟合出来的直线100%经过坐标原点(0,0)
所以,不要太着急,在这里做去平均值还是非常有用的,因为它能帮我们把整个坐标的原点移到散点图的中间,画个图给大家理解一下:
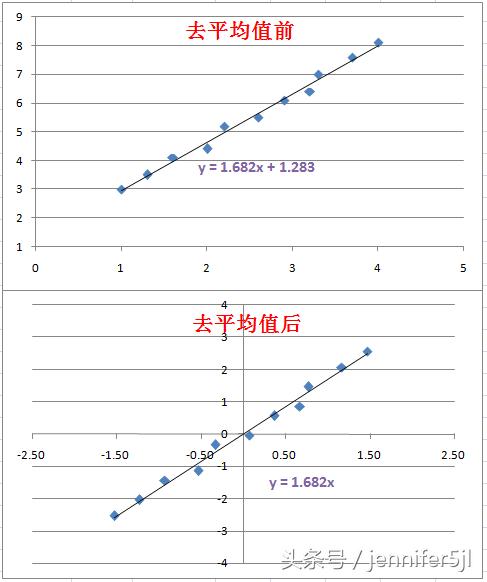
然后,按着公式做矩阵计算,这里为了写得简单点,公式前面标识的x指的都是已经去平均后的x-m

公式部分给大家放大一点:
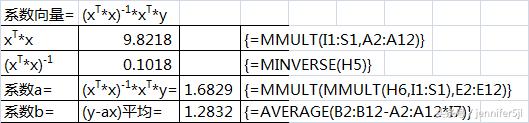
到这里计算就结束了,但是,为什么要用这么麻烦的解法来计算一条直线呢?难道是吃饱了撑的?
当然不是,向量化的计算方法比其他一般的解法有一个最明显的优势——就是它支持同时有多列x的输入值,像这样:

像这种情况下,Excel自带的什么画图啊,斜率截距公式什么的肯定就废了
例子都举了(虽然是用随机数生成的),那就再做一个看看呗
公式形式:y=b a1x1 a2x2 a3x3 a4x4,走起

这样是不是反而比正常的方式来得更简洁了呢?
,




