我被学生提问难住了——几何填空压轴题思路探索

作为数学老师,解题是家常便饭,而遇到一时解不出来的题也并不少见,于是,分析自己解题思路受阻于何处,如何突破,进而领悟如何去引导学生。当然,被学生所提问题当场问住,的确也有些难堪,不过面子不重要,既然遇到困难,和学生一起思考,在这个过程中,其实也是教育学生,老师也会遇到一时想不出来的难题,此时示范给学生,如何才是面对困难不放弃。
题目
点P是△ABC内一点,∠PBC=30°,∠PBA=8°,且∠PAB=∠PAC=22°,则∠APC=_________°.
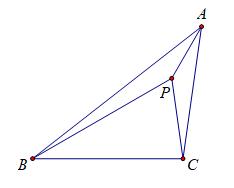
我的探索一:
将所有能求的角全都求出来,△ABC中,∠ABC=38°,∠ACB=98°,∠BAC=44°,进一步求得∠APB=150°,然后尝试寻找∠APC与这些已知角的关系,设∠APC=x,则∠ACP=158°-x,∠BCP=x-60°,∠BPC=210°-x,然后便再也找不出等量关系了,探索失败!
我的探索二:
仅仅寻找角之间的等量关系是不够的,需要找到新的等量关系,方程才能列出来,看到AP两边∠PAB=∠PAC之后,联想到角平分线,延长试下?

继续表示新出现的角,∠DPB=30°,∠PDC=60°,∠DPC=180°-x,又无路可走了,和探索一出现的困难一样,没有找到新的等量关系列方程求解,探索失败!
我的探索三:
是否需要构造全等三角形转化角呢?利用角平分线,的确可以很方便地构造,在AB上截取AE=AC试下?

这次收获比前两次要大一点,图中△APE≌△APC很容易证明,然而看上去似乎相等的BE和PE,始终没办法证明,探索失败!
我的探索四:
不急,角平分线一定是突破口,于是角平分线有哪些性质?角平分线上的点到角两边距离相等?好,便是它,再来!

在角平分线上,不同的点都尝试过一遍,全等三角形非常容易找到,可是问题依旧没解决,看来仅仅依靠角平分线性质构造出的全等三角形,并不足以找到新的等量关系,探索失败!
我的探索五:
陷入沉思后,回顾刚刚的探索过程,失败了四次,并不是一点作用都没有,至少基本方向确定了,角平分线一定能构造全等三角形,如果还能构造出特殊三角形,就能找到新的等量关系了。
等等!刚刚计算出的角度中,含有特殊角30°,60°,包含这种度数的三角形中,等边三角形最特殊,而等边三角形中,三线合一,其中一线正好就是角平分线啊!
仿佛受到启发,在前面探索图形基础上,又进行了调整。

将角平分线AP延长,然后过点B作它的垂线,垂足为E,交AC延长线于点F,再连接PF。
其实和前面探索中某一个图形很像,只是所连线段不同,这样作辅助线的好处是,全等三角形依然非常容易找到,此时图中的△ABF是等腰三角形,AE是BF的垂直平分线,于是可证△APB≌△APF,在Rt△ABE中,我们可求出∠ABE=68°,于是∠PBE=60°,因此△BPF是等边三角形,设想的目的已经达到了。
继续推导,在等边△BPF中,BC是PF的垂直平分线,于是CP=CF,所以∠PFC=∠FPC,前面已经证明的全等三角形可求得∠PFC=∠PBA=8°,因此∠FPC=8°,而∠EPF=30°,所以∠APC=180°-30°-8°=142°.
解题反思:
原来垂直平分线才是解这道题的关键!回过头来看前面失败的四次探索,无一次构造出了垂直平分线,都在角平分线性质和全等三角形内转圈。而学生在思考过程中,也同样经历了失败,例如探索一和探索二,学生也尝试过,因此这两种思路我也只是简单目测了一下,感觉不行,便没有继续浪费时间。然而构造全等三角形时,角平分线实在是太方便,所以就没有继续思考还有没有其它特殊图形,直到所有路都走死了,只好转身继续深挖条件。
失败的探索中,并非没有益处,至少最后想到垂直平分线,还得多谢第四次失败,当等腰三角形三线合一条件一出现,下意识感觉思路明朗了。因此在面对角平分线条件的时候,除了角平分线本身的性质之外,还需要联系和它有关的定理。
当我在草稿纸上不断尝试推演时,学生一直在旁边看着,不发一言,倒是我自言自语很多,最终当我抬起头告诉学生,我解出来的时候,他脸上是崇拜和敬重,而不是我以为的嘲笑和轻蔑。
给学生讲这道题,除了收获解法之外,我想更重要的是做人的道理,正如我有困难求助于他人,而他人也在努力解决我的问题中遇到困难,我不可能在一旁嘲笑,而是要鼓励与支持,提供力所能及的帮助,这才是正道。
爱数学做数学





