撰文 丘成桐
我很荣幸师从一位伟大的数学家。陈省身对我的学术生涯,无论数学上还是个人修养方面,都有着深刻的影响。
回顾微分几何的发展历史,我认为嘉当(E. Cartan)是微分几何的祖父,陈省身是现代微分几何之父。他们合力创造了一门美妙而丰富的学科,影响遍及数学与物理的每个分支。

(左)埃利·嘉当(1869~1951)、(右)陈省身(1911~2004)
在去世前,陈省身说他就要去见古希腊那些伟大的几何学家了。毫无疑问,他的成就堪与这些大几何学家比肩。
我们现在来回顾几何学发展史上的重要事件。从这些历史事实,我们也可以看到这两位伟大的几何学家在数学史上的崇高地位。
-
古希腊早期的毕达哥拉斯学派(Pythagoras,约公元前580~前500),发现并证明了:直角三角形的两条直边的平方和等于斜边的平方。西方称这一命题为毕达哥拉斯定理。中国古代也有同样的发现,因而在中国称之为勾股定理。
-
古希腊几何学家欧几里得(Euclid,约公元前330~前275),写出了著名的《几何原本》,建立了公理化的欧几里得几何体系。
-
古希腊数学家阿基米德(Archimedes,约公元前287~前212),用类似于现代积分学的方法,计算物体的面积与体积。

法国哲学家、数学家笛卡儿(René Descartes,1596~1650)引入坐标,解析几何诞生,代数与几何走向融合。
法国几何学家德萨格(Gérard Desargues,1591~1661)创立了射影几何。
法国数学家费马(1601~1665)在研究光学时,发现了变分原理。

自左至右依次为:笛卡儿(1596~1650)、德萨格(1591~1661)、费马(1601~1665)
-
英国数学家巴罗(I. Barrow,1630~1677)、牛顿(Isaac Newton,1642~1727)和德国哲学家、数学家莱布尼茨(Gottfried Wilhelm Leibniz,1646~1716)将微分与积分融合起来。(微分与积分的思想在古希腊,古印度,古代中国,阿拉伯等国就已萌芽。不过,这些早期的发展未能将微分与积分联系起来。)

自左至右依次为:巴罗(1630~1677)、牛顿(1642~1727)、莱布尼茨(1646~1716)
-
瑞士数学家欧拉(Leonhard Euler,1707~1783)发明组合几何并发展变分法。
-
德国数学家高斯(Carl Friedrich Gauss,1777~1855)开创了内蕴几何。
-
德国数学家黎曼(Bernhard Riemann,1826~1866)1854年在为取得教师职位所做的演讲中,提出了黎曼几何的思想。

自左至右依次为:欧拉(1707~1783)、高斯(1777~1855)、黎曼(1826~1866)
-
挪威数学家索菲斯·李(Sophus Lie,1842~1899)创建了变换群理论,并发现了切触几何。
-
德国数学家克莱因(Felix Klein,1849~1925)在1872年宣布了埃朗根纲领,把几何定义为研究各种变换群作用下的空间。

(左)索菲斯·李(1842~1899)、(右)克莱因(1849~1925)
-
例如,射影变换群对应的几何是射影几何,主要的贡献者包括庞斯莱(Jean-Victor Poncelet,1788~1867)、默比乌斯(August Ferdinand Möbius,1790~1868)、沙勒(Michel Chasles,1793~1880)和施泰纳(Jakob Steiner,1796~1863)。
-
还有仿射几何与共形几何,它们分别对应于仿射群和共形群。

自左至右依次为:庞斯莱(1788~1899)、默比乌斯(1790~1868)、沙勒(1793~1880)、施泰纳(1796~1863)
嘉当和陈省身继承了这些伟大几何学家的事业,凭着他们的几何直觉创造了20世纪微分几何的基础。
法国数学家安德烈·韦伊(André Weil,1906~1998)在为《陈省身论文选集》撰写的序言《我的朋友——几何学家陈省身》一文中写道:
真正的几何直观在心理上也许永远说不清楚……无论如何,如果没有嘉当、霍普夫、陈省身和另外几个人的几何直觉,本世纪的数学决不可能有如此惊人的进展。我深信,只要数学继续发展,就永远需要这样的数学家。
现代微分几何的诞生
嘉当的工作 嘉当继高斯、黎曼、李和克莱因之后完成了为现代微分几何奠基的工作。通过把他关于李群和微分方程组不变量理论结合起来,他引入了现代规范理论。
嘉当定义了广义空间,包括了克莱因的齐性空间与黎曼的局部几何。用现代术语来说,就是“纤维丛上的联络”。这推广了列维-齐维塔平行性的概念。
一般而言,我们有一个纤维丛 π : E → M,其纤维 π-1(x )(x ∈ M ) 是有李群 G 作用的齐性空间。一个联络就是纤维上与群G 作用相容的无穷小移动。
格拉斯曼引入了外形式,而嘉当引进了外微分运算。他的 Pfaff 方程组理论和延拓理论创造了可以用来解决几何中等价问题的不变量。
嘉当用活动标架构造不变量的观点对陈省身有很深的影响。陈非常欣赏活动标架法,甚至他九十岁时还在国内讲授这个理论。

(左)韦伊(1906~1998)、(右)霍普夫(1894~1971)
霍普夫的工作霍普夫(Heinz Hopf,1894—1971)最早开始研究微分拓扑,如流形上的向量场。他的学生斯蒂弗尔(E. Stiefel)推广了霍普夫的定理,得到了斯蒂弗尔-惠特尼(Stiefel-Whitney)示性类。
1925年,霍普夫在他的论文中研究了超曲面情形的高斯-博内定理。1932年,霍普夫强调指出被积函数可以写成关于黎曼曲率张量分量的多项式。
这些工作深刻影响了陈省身后来的工作。
霍奇(W. V. D. Hodge)、庞特里亚金(L. S. Pontryagin)和惠特尼(H. Whitney)的工作 他们都是伟大的微分拓扑学家,后两位在示性类上的贡献直接影响了陈氏类的产生。
陈省身:整体内蕴几何之父
陈省身说过,黎曼几何及其在微分几何中的推广有局部的特征。让我感觉很神秘的是,我们确实需要一个整体的空间把每片邻域连接起来。这可以用拓扑来完成。
嘉当和陈省身都看到了纤维丛在微分几何中的重要性。当然,许多大数学家都研究过整体微分几何,如科恩-沃森(Cohn-Vossen)、闵可夫斯基(H. Minkowski)、希尔伯特(D. Hilbert)、外尔(H. Weyl),但是他们的工作主要局限在三维欧氏空间中的曲面的整体性质。
陈省身在内蕴几何与代数拓扑之间建立了桥梁。(嘉当在微分几何上的工作在本质上更强调局部,除了他在对称空间方面的工作。)
陈省身接受的教育
(南开大学和清华大学)
他在天津南开大学读大学本科,接着在北京清华大学读研究生。在此期间,他学习了库利奇(J.L. Coolidge)的《非欧几何》和《圆周与球面的几何》,萨蒙(W. Salmon)的《圆锥曲线》和《立体解析几何》,卡斯泰尔诺沃(G. Castelnuovo)的《解析几何与射影几何》,以及斯坦德(Otto Stande)的《线构造》。
他的硕士生导师孙鎕研究射影微分几何,该领域由维尔辛斯基(E.J. Wilczynski)于1901年创立,后来被富比尼(G. Fubini)和切赫(E. Cech)发展。
陈省身的硕士论文是关于射影线几何,即研究三维射影空间中所有直线组成的空间的超曲面。他研究了线汇,即线的二维子流形以及它们的通过二次线体的密切。
陈省身接受的教育(布拉施克)
1932年,布拉施克访问北京。他做了题为“微分几何中的拓扑问题”的演讲,主要讨论了微分同胚伪群及其局部不变量。陈省身开始考虑整体微分几何,并且认识到代数拓扑的重要性。他读了维布伦(O. Veblen)的书《位置分析》(Analysis Situs,1922)。
1934年,他去德国汉堡大学跟随布拉施克学习。阿廷(E. Artin)、赫克(E. Hecke)和凯勒(E. Kähler)也在那里。布拉施克那时主要研究网几何与积分几何。陈省身开始研读赛弗特-特雷法尔(Seifert-Threlfall)的《拓扑学讲义》(1934)和亚历山德罗夫-霍普夫(Alexandroff-Hopf)的专著《拓扑学》(1935)。
陈省身接受的教育(凯勒、嘉当)
在汉堡大学时,凯勒在讨论班上讲解了他写的小册子《微分方程组理论导引》,就是现在所称的凯勒-嘉当理论。陈省身是这个讨论班的忠实学生。
1936~1937年,陈省身来到法国巴黎,跟随嘉当研究活动标架法和等价方法,并且更深入研究了凯勒-嘉当理论。他在巴黎逗留了十个月,每两周与嘉当会面一次。
陈省身于1937年夏回到中国。他用了几年时间研究嘉当的工作。他曾说,嘉当一生中的论著超过三千页,他至少读过其中的百分之七八十。有一些文章他反复研读过好多次。在战争年代的孤立环境下,很容易做到全身心地阅读和思考。
陈省身评价嘉当说:“他毫无疑问是本世纪最伟大的数学家之一,他的学术生涯体现出了一种罕见的睿智与谦逊的融合。1940年,我努力研读嘉当的著作,意识到联络的概念将会发挥重要的作用,于是我写了几篇论文,对一个给定的几何结构配上联络。”
陈省身几乎是唯一的能够很好掌握嘉当工作的几何学家。甚至像外尔那样的大师都认为嘉当的论著很难读。外尔说:“嘉当无疑是微分几何领域仍然健在的最伟大的人物……不得不承认的是,我发现嘉当的书和他的大多数论文一样,艰深难读……”
等价问题
陈省身的大多数工作与等价问题有关。1869年,克里斯托费尔(E. Christoffel)和利普希茨(R. Lipschitz)解决了黎曼几何中的等价问题,这个有着基本重要性的问题被称为“形式问题”:为了确定两个 ds2 是否只相差一个坐标变换,克里斯托费尔引入了现在被称为列维-齐维塔联络的协变微分。
嘉当把这个问题推广到更一般的情形,被称为等价问题。
等价问题 给定分别在坐标 xk,x*l 下的两组线性无关的线性微分形式 θi, θ*j,其中 1≤i, j, k, l ≤n;给定一个李群

,要求找到合适的条件,使得存在函数
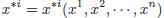
,并且 θ*j 在经过如上替换后,与相差 G 中的一个变换。
这个问题与局部不变量有关,嘉当给出了生成这些不变量的具体步骤。陈的大部分工作都与这个问题有关。
陈省身(1932—1943)
在此期间,他研究了网几何、射影线几何,射影空间中子流形对的切触不变量以及孤立子理论中的贝可隆(A.V. Bäcklund)变换有关的曲面变换。陈省身后来在与格里菲思(P. Griffiths)和滕楚莲的合作中,继续这方面的研究。
陈省身在他的博士论文中研究了射影微分几何。简单来说,这个学科的一个基本问题是:找到子流形在射影变换群下的一族完全的局部不变量,并用与简单几何图形的密切来给出几何上的解释。
射影几何中的另一个典型问题是,用正规射影联络研究道路结构的几何。例如,索菲斯·李的学生特雷斯(Tresse)用空间(x, y, y')中的正规射影联络研究了由积分曲线 y'' = F(x, y, y')定义的道路。
陈省身把上面的工作推广到 n 维。给定满足一组微分方程的 2( n-1)维曲线族,使得在每一点给定一个方向,正好有一条这样的曲线和它相切。陈定义了正规射影联络,把结论推广到子流形族。
1940~1942年期间,陈省身开始推广由克罗夫顿(M.W. Crofton)和布拉施克发展起来的积分几何。他注意到,这种几何可以用具有相同李群 G 的两个齐性空间来更好地加以理解。于是,有 G 的两个子群 H 与 K,满足

。
两个陪集 aH 与 bK 称为互相关联,如果它们在 G 中相交。用这种方法,他推广了克罗夫顿的许多重要公式。1952年,他推广了庞加莱、桑塔洛(L.A. Santaló)和布拉施克的运动公式。
韦伊评价陈省身的一篇有关文章:它把布拉施克学派的工作一举推进到更高的水平。文章所显现的非凡才能和深刻见解给我留下了很深的印象。
陈省身对普林斯顿的访问(1943)
1943年,陈受到维布伦和外尔的邀请,从昆明前往普林斯顿。外尔是陈心目中的英雄。纤维丛理论发端于嘉当和惠特尼的工作。斯蒂弗尔-惠特尼示性类只在模 2 同调上有定义。韦伊当时刚刚发表了他关于高斯-博内公式的论文,他把托德和埃格尔关于代数几何中典则类的工作告诉了陈。这些工作秉承了意大利代数几何学派的风格,用到了一些未经证明的结果。
陈省身所做的第一项基本重要性的工作就是给出了高斯-博内公式的内蕴证明。这个公式的简约历史可以叙述如下:
高斯在其开创性论文《关于曲面的一般研究》(Disquistiones Circa Superficies Curvas,1827)中,首先求出了关于测地三角形的公式:他考虑的是中的曲面,并且用了高斯映射。
博内(O. Bonnet)在1848年的一篇论文(Mémoire sur la théorie générale des surfaces, J. De l’Ecole Poly. Tome 19, Cahier 32 (1848) 1-146.)中,把高斯的公式推广到以一条任意曲线为边界的单连通区域。
戴克(W. Dyck)在1888年(Beiträgezur analysis situs, Math Annalen 32(1888) 457-512.),把高斯-博内公式推广到任意亏格的曲面。
1925年,霍普夫把公式推广到

中的余维数为 1 的超曲面。1940年,艾伦多弗(C.B. Allendoerfer)和费恩雪尔(W. Fenchel)研究了可以嵌入到欧氏空间中的可定向闭黎曼流形。1943年,艾伦多弗和韦伊把公式推广到闭黎曼多面体,也即一般的闭黎曼流形。但证明仍然要用到流形到欧氏空间的等距嵌入。
韦伊把他们的工作和陈省身的工作做了比较:基于外尔和其他一些人的工作,我们的依赖于“管子”的证明虽然的确要用到(当时还不明了)球丛的构造,也就是一个给定浸入的横截丛,但不是内蕴的。陈的证明第一次清楚地引入了内蕴丛,也就是单位长度的切向量丛上的运算,让整个领域的面貌焕然一新。
一个世纪前,高斯建立了内蕴几何的概念。陈的关于高斯-博内定理的证明开创了全新的领域。整体拓扑通过纤维丛以及切球丛上的超渡,与内蕴几何建立了联系。我们看到了整体内蕴几何揭开了崭新的一页。
以下我们来看,陈省身的证明甚至在二维情形都是全新的。
利用活动标架,曲面的结构方程可以写为

这里 ω12 是联络形式,K 是高斯曲率。如果单位向量 e1 由一个整体定义的向量场 V 按如下给出:
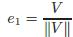
其中在 V ≠ 0 处有定义。应用斯托克斯公式可以得到

其中 B(xi) 是一个以 xi 为圆心的小圆盘,并且

可以用向量场 V 在 xi 处的指标来计算。根据霍普夫的一个定理,向量场的指标之和等于空间的欧拉数。这样曲面上曲率的积分就给出了欧拉数。
在高维的情况下,陈省身的证明中用到的是单位切球丛。曲率形式 Ωij 是反对称的,其 Pfaffian 形式是

相应的高斯-博内公式是

为了证明高斯-博内公式,必须找到单位球丛上的形式 Ⅱ,使得 Ⅱ 是 Pf 的提升。虽说陈省身的证明受到霍普夫向量场定理的启发,但充分反映了陈省身过人的洞察力与精湛的运算技巧。霍普夫曾说过,陈的证明把微分几何学带入了一个崭新的时代。特别是诞生了“超渡”的概念。这是现代数学史上最了不起的工作之一。
陈类
陈省身说:“我最早接触示性类,是由于高斯-博内公式,这是每个学过曲面论的人熟知的公式。早在1943年,当我给出维高斯-博内公式的内蕴证明以后,我认识到,应用曲面论中的正交标架,那么经典的高斯-博内公式不过是高斯绝妙定理的一个整体性的结果。这个证明的代数方面是后来被称为‘超渡’的构造的第一个实例,超渡注定了会在纤维丛同调论和其他一些问题中扮演基本重要的角色。”
嘉当关于标架丛的工作,德·拉姆定理,它们始终隐藏在陈省身思想的背后。纤维丛是现代数学的核心概念,它把许多重要的数学和物理对象统一起来。以下我简单描述一下纤维丛的历史。
斯蒂弗尔(1936)和惠特尼(1937)引入了斯蒂弗尔-惠特尼示性类,但它只在模 2 的情形下有定义。
费尔德保(J. Feldbau)(1939)、艾瑞斯曼(C. Ehresmann)(1941,1942,1943)、陈省身(1944,1945)和斯廷罗德(N. Steenrod)(1944)系统研究了纤维丛的拓扑。
庞特里亚金(1942)引入了庞特里亚金示性类。他还在1944年把黎曼流形的曲率与拓扑不变量建立联系(发表在 Doklady 杂志上)。这依赖于流形的嵌入,他开始并没有意识到这些不变量就是庞特里亚金类。
在高斯-博内公式的证明中,我们可以找到 k 个一般位置的向量场 s1, …, sk 。它们线性无关的点构成了一个与 si 的选取无关的(k-1)维闭链。这是斯蒂弗尔的工作(1936)。惠特尼(1937)考虑了更一般的球丛的截面,从阻碍理论的角度对它们加以理解。
惠特尼注意到

中 q 平面组成的格拉斯曼流形 G( q, N ) 上的万有丛的重要性。他在1937年证明,流形上的任意秩为 q 的丛都可以由 G( q, N ) 上的万有丛经过映射 f : M → G( q, N ) 来诱导。
当 N 很大时,庞特里亚金(1942)和斯廷罗德(1944)注意到映射只相差一个同伦。丛的示性类按如下给出:

上同调 H*(Gr(q, N )) 由艾瑞斯曼(1936)做了研究,它们可以由舒伯特胞腔生成。
陈省身当时大概想证明庞氏的曲率不变量就是庞氏类,但在实的情形下,舒伯特的胞腔比较复杂。
陈省身说:“也许略带幸运,我在1944年注意到了一个平凡的事实,复向量丛的情形要比实的情形简单许多。因为大多数经典的复空间,如经典的复的格拉斯曼流形,复的斯蒂弗尔流形等都是无扭的。”
对复向量丛 E,陈省身因此引进了陈类 。陈省身用三种不同的方法加以定义:阻碍理论、舒伯特胞腔以及丛上联络的曲率形式。他证明了这些方法的等价性。陈氏类成为近代数学最重要的不变量。
陈省身的基本论文(1946)
在文章《埃尔米特流形上的示性类》(Characteristicclasses of Hermitian manifolds)中,陈为复流形的埃尔米特几何奠定了基础。比如,他引入了埃尔米特联络的概念。如果 Ω 是向量丛的曲率形式,我们定义

。
用微分形式定义陈类,对几何学与现代物理都有极为重要的意义。一个例子就是陈省身创造的超渡的概念。
超渡(Transgression)令φ 是在与向量丛相配的标价丛上定义的联络形式,那么曲率形式为
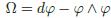
所以

类似的
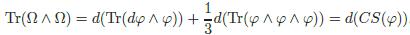
其中 CS(φ) 称为陈-西蒙斯形式,在三维流形、反常消除问题、弦理论、固态物理中起着基本重要的作用。
在微分形式的层次上做超渡引出了同调群上的二级运算。比如,梅西乘积,这出现在陈国才关于迭代积分的工作中。
当流形是复的,我们记

。
在一篇重要的文章中,博特(R. Bott)-陈(1965)发现,存在一个典则构造的(i-1,i-1)形式
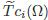
, 使得

。
陈省身应用这个定理推广了高维复流形间全纯映照值分布的奈旺林纳(R.H. Nevanlinna)理论。
微分形式
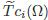
后来在阿莱克勒夫(S.J. Arakelov)理论中起了基本的作用。
唐纳森(S.K. Donaldson)用的情形证明了关于代数曲面上埃尔米特-杨-米尔斯联络存在性的唐纳森-乌伦贝克(K. Uhlenbeck)-丘定理。
当 i = 1 时,

,
其中

是埃尔米特度量,等式右边是度量的里奇张量。第一陈类是如此简洁,这促使卡拉比(E. Calabi)提出了他的著名猜想。
陈类的曲率表示意味着陈数可以通过曲率的积分得到。这使得Hirzebruch可以用局部对称空间来推导比例性原理,即覆盖空间与底空间的陈数之比正比于与体积之比。类似的,这也启发我用凯勒-爱因斯坦度量给出了米姚卡-丘不等式的证明。所有这些定理都是以陈类的曲率表示为前提的。
正如陈省身所说的那样,复数域上几何的简洁与美妙无论如何也不会被夸大。
陈省身(战后回国)
陈省身在普林斯顿完成了两项杰出的工作后,于1946年4月回到中国。国民政府聘请他到中央研究院数学研究所,协助他以前在南开的老师姜立夫。姜立夫担任所长,但主要由陈省身负责数学研究所的日常事务。陈省身讲授当时拓扑学研究的前沿课题。有许多学生和博士后参加他的讨论班,包括陈国才、王宪忠、吴文俊、杨忠道、,严志达等。许多人后来成为中国数学的领军人物。
陈省身(芝加哥的岁月)
1948年12月31日,在维布伦和外尔的邀请下,陈省身离开上海,前往普林斯顿高等研究院,并在那里停留了一个冬天。我的印度朋友告诉我,塔塔研究所曾想聘请陈省身,但是没有成功。陈到普林斯顿后,芝加哥大学的斯通(M. Stone)教授向陈省身提供了一个教授职位。陈的朋友韦伊在其中起了重要的作用。他很快在芝加哥安顿下来,并与韦伊一起开设讨论班,参加者中有辛格(Singer)、斯特博格(Sternberg)、卡迪森(Kadison)。陈对美国几何学影响深远。辛格一直尊称陈是他的老师。在这段时期,他培养了几个杰出的学生,如廖山涛、沃尔夫(J. Wolf)和野水(Nomizu)。
在1946年发表了关于陈类的重要文章后,陈省身详细研究了示性类的乘积结构。
1951年,他与斯帕尼尔(E. Spanier)合作了一篇关于纤维丛上吉森(W. Gysin)序列的文章。他们独立于托姆(R. Thom)证明了托姆同构。
分裂原理
陈省身在1953年的文章《关于复球丛和代数簇的示性类》(On the characteristic classes of complex spherebundle and algebraic varieties)中,通过考虑以旗流形作为纤维的相配丛,证明了示性类可以用线丛来定义。作为一个推论,代数流形的示性类的对偶同调类包含一个代数闭链的表示。这篇文章提供了理论中的分裂原理,将其与托姆同构结合,就可以给出相配丛上陈类的定义,如同格罗登迪克(A. Grothendieck)后来所做的那样。
霍奇曾经研究过用代数闭链表示同调类的问题。他考虑过上述陈省身的定理,但只能证明当流形是射影空间中非奇异超曲面的完全交时的情况。
陈省身的上述定理是最早的,而且是关于“霍奇猜想”的唯一已知的一般陈述。它还提供了全纯K-理论和代数闭链之间的直接联系。
陈与拉萧夫(R. Lashof)合作研究了欧氏空间超曲面紧贴嵌入(tight embedding)的概念。这项工作后来由柯伊伯(N. H. Kuiper)和班考夫(T. F. Banchoff)做了推广和延拓。
伯克利的岁月和回归祖国
1961年,陈省身前往伯克利,直到1979年退休。他退休后还继续留在数学系任教三年。陈省身和 Smale 来到伯克利的时候,正是伯克利大学数学系崛起成为世界数学中心的时期,在 Evens、Tarski、 Morrey、Kelly 等人的努力下,伯克利聘请了许多著名数学家。此后,陈省身聘请了许多杰出的几何拓扑学家,使得伯克利迅速成为几何与拓扑学的中心。
陈省身在伯克利期间培养了许多杰出的学生,包括 Garland、Do Carmo、Shiffman、Weinstein、Banchoff、Millson、郑绍远、李伟光、Webster、Donnelly 和 Wolfson 等。陈的学生们也受益于陈的朋友和他早期的学生。比如,Garland 得到王宪宗的指导,Millson 得到西蒙斯的指导。陈的个人魅力深刻影响着在伯克利 Campbell 大楼和 Evans 大楼工作的这些杰出几何学家群体。伯克利的几何讨论班和研讨会总是挤满了学生、教员和访问学者。众所周知的是,每个伯克利的访问学者都会被陈邀请到中餐馆享用一顿难忘的晚宴,或者在他家中受到热情款待。陈太太总是用中式美食欢迎每一个客人。伯克利的这段时光让整整两代几何学家铭记。
在伯克利,陈省身与卡拉比和奥瑟曼(R. Osserman)合作研究极小曲面理论。他也尝试推广奈旺林纳理论,从而发现了博特-陈形式与陈-莱维-尼伦伯格内蕴范数,这些工作在复几何中发挥了意想不到的作用。他与西蒙斯的工作深刻影响了几何学与物理,包括扭结理论。他与莫泽(Moser)关于复欧氏空间中实超曲面局部不变量的理论在多复变函数论中具有基本的重要性。陈与格里菲思推广了陈早期在网几何上的工作。网几何是陈的老师布拉施克,以及Thomsen创立的,他们注意到平面上的三族曲线纤维化具有局部不变量。陈省身对网几何钟爱有加,这从他在1982年为美国数学会通报撰写的文章就可以看出。
在20世纪80年代初期,陈省身与辛格(I.M. Singer)、莫尔(E.H. Moore)共同创建了伯克利数学研究所。他退休后返回中国,在南开大学创办了陈省身数学研究所,对中国数学发展产生了深远影响。
结束语
陈省身有着惊人的为重要几何结构创造不变量的才能,在我所认识的数学家中,无人能出其右。他在射影微分几何、仿射几何与拟凸域的陈-莫泽不变量的工作展示了他的能力。他与莱维、尼伦伯格定义的复流形上同调的内蕴范数还有待发掘。在他去世前,他的一个主要工作设想就是把嘉当-凯勒系统推广到更一般的几何情形。
陈省身曾经说:“几何中复数的重要性对我而言充满神秘。它是如此优美简洁而又浑然一体。”他总是对古代的中国数学家从未发现复数抱憾不已。令人欣慰的是,陈省身在复几何上影响深远的工作足以弥补过去两千年中国数学的缺憾。
天文学家将一颗小行星命名为“陈省身星”。希望他的光辉能够一直照耀未来的中国数学家。
本文刊登于《数学与人文》丛书第3辑《陈省身与几何学的发展》,高等教育出版社 & International Press of Boston,2011. 《赛先生》经“数学与人文”丛书(微信订阅号:math-humanity)授权转载。
投稿、授权等请iscientists@126.com
赛先生系今日头条签约作者
,