女士们,先生们,老少爷们儿们!在下张大少。
定义和基本属性
图1中的曲线称为心形线。心形线有许多有趣的性质,经常出现在不同的数学和物理领域。研究曲线的几何性质是解析几何和微分几何中的一个经典课题。在这篇文章中,我们主要关注心形线的合成方法。

图1
在极坐标下,心线线方程为:
r = 1 − cos ϕ
在本文中,我们考虑了心形线的几何性质,所以让我们给出一个几何定义。取一个直径为1的圆,让另一个同样大小的圆在第一个圆的外面滚动。那么第二个圆上一个不动点的轨迹将是一条心线(图2)。
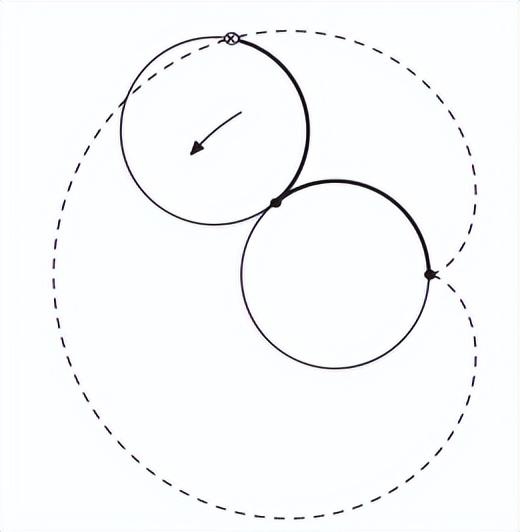
图2
这一定义在研究心形线时不太有用,所以我们纯粹从几何角度重申这一定义。设ω为以O为圆心的圆,A为圆上的一点,P为沿ω运动的点(图3)。设O为P中与O对称的点,设B为A在OO‘的垂直平分线上的反射。注意到∠BO’P =∠POA,O’B = OA。那么,点B的轨迹是一条心线。
点A称为心形线的尖点,心形线与射线AO交点V称为顶点(图3)。
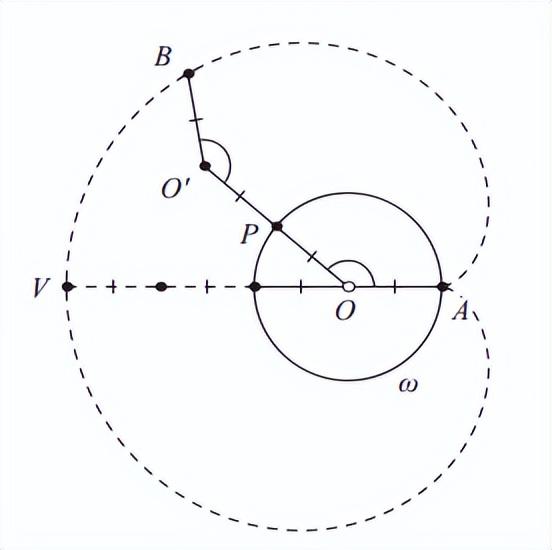
图3
因为三角形AOP是等腰的,AB平行于OP,所以一个简单的角度对应关系如下所示。
引理1:AP是角OAB的平分线。
用Q表示AB和ω的第二个交点(图4)。请注意,在四边形BO’OQ中,两条对边是平行的,另外两条是相等的。因此,它是一个平行四边形或等腰梯形。但它不是等腰梯形,因为在这种情况下它将与AOO’B重合。因此,BQ等于O’O,又等于圆ω的直径。如果角AOP是锐角,那么点Q位于线段AB之外,结构看起来与图4有些不同。但在这种情况下,证明与所考虑的情况类似。

图4
因此,我们得到一个心形线的运动学定义。让ω是一个直径为1的圆,A是其上的一个点。让我们取一个沿ω移动的点Q。让B是AQ线上的一个点,使BQ等于1,即ω的直径(图5)。那么B就沿着一条心形路径移动。B点有两个选择(在点Q的两边)。这两个点都位于心形路径上。从这个结构中,我们很容易看出,这条曲线是由以A为中心的极坐标系中的方程(*)定义的。

图5
心形线的切线。心形线的切线怎么做?让我们回到最初的定义,假设一个圆围绕ω旋转,在某个时刻,这两个圆在P点相互接触(图6)。怎么才能找到标记点B的速度矢量的方向?从力学上我们知道P点(在圆ω上)的速度等于零,该点处于静止状态。点B的速度垂直于线段BP,因为点B和P之间的距离不变。我们得到下面的陈述。

图6
引理2:心形线在B点的切线垂直于BP。
因此,心形线触及所有以圆ω上的点p为圆心、半径为PB = PA的圆。换句话说,心形是这个圆族的包络(图7)。

图7
另外,这个心形线图案也经常出现在咖啡杯中。来自顶点V的光线在圆的内部反射后,沿着心形的切线传播(图15)。换句话说,如果有光源在其上,心形就是圆的焦散线。所以在日常生活中遇到它是可能的(图16,)。你可以自己尝试下面的实验。拿一个金属锅,在锅边放一个打火机。从边缘反射回来的光线会在锅底画一个心形。

图15

图16 https://en.wikipedia.org/wiki/File:Caustique.jpg
关于心形的另一个有趣的事实是,它是著名的Mandelbrot集的中心部分(图17,Wolfgang Beyer拍摄的图片)。要了解更多细节,我们推荐书[3]。

图17 https://en.wikipedia.org/wiki/File:Mandel_zoom_00_mandelbrot_set.jpg
最后欣赏一下心形线和它的远房亲戚心窝线的美图。

参考文献
1. R. A. Johnson,Advanced Euclidean Geometry. Dover Publications, Mineola, NY, 2007.
2. X. Lee, Cardioid, http://xahlee.info/SpecialPlaneCurves_dir/Cardioid_dir/cardioid.html.
3. H. Peitgen, P. Richter, The Beauty of Fractals: Images of Complex Dynamical Systems. Springer-Verlag, Berlin, 1986.
青山不改,绿水长流,在下告退。
转发随意,转载请联系张大少本尊。
,




