
大自然生物的美,总是给人以美的享受,就像蝴蝶一样,对称的体型,美丽的翅膀,总能让人心情舒畅。今天,我们走进数学的殿堂,来一起认识一下另一种蝴蝶。连接任意一个四边形的对角线,会将四边形分成四个部分,它的形状类似于蝴蝶,称之为“蝴蝶模型”,其背后关于面积和边的比例性质引出了一系列定理,称之为“蝴蝶定理”。
一、任意四边形中的比例关系(“蝶形定理”)

★结论1:如图所示,ABCD是任意一个四边形,被两条对角线分成了四部分,其面积分别为S1、S2、S3、S4,则有:

☞上述结论的得出依据有两个:一是等高三角形面积之比等于对应的底之比。即:S1:S2=DO:OB=S4:S3。二是比例的基本性质。即在比例里,两个外项的积等于两个内项的积。由S1:S2=S4:S3可得外项积=S1×S3,内项积=S2×S4,从而得出结论。第②个结论的得出也是依据比例的一些性质,综合计算得出来的,因为:S1:S4=S2:S3= AO:OC(设其等于a),则S1=a×S4,S2=a×S3,从而(S1 S2)÷(S4 S3)=a =AO:OC
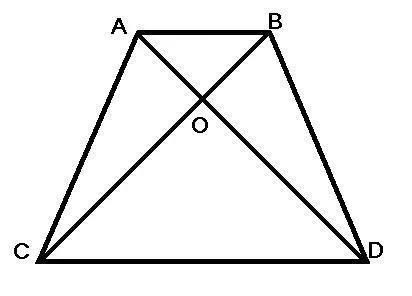
二、梯形中比例关系(“梯形蝶形定理”)

★结论2:如图所示,ABCD是梯形,被两条对角线分成了四部分,其面积分别为S1、S2、S3、S4,则有:

结论①的证明需要借助:平行线分线段成比例性质及其推论(内容附后)以及鸟头模型。根据平行线分线段成比例性质及其推论,可得,AO:OC=DO:OB=a:b,根据鸟头模型,可知:S1:S3=(AO×OD):(BO×OC )=a²:b²,结论②和③方法相同。

三、具体应用
蝶形定理为我们提供了解决不规则四边形的面积问题的一个途径.通过构造模型,一方面可以使不规则四边形的面积关系与四边形内的三角形相联系;另一方面,也可以得到与面积对应的对角线的比例关系.
例题:



练习题及答案








