在上一篇文章中,我们介绍了代数式书写的六项注意点,这是整章的基础,千万不能出错。注意点为:当数字与字母相乘时,乘号省略不写,并且数字要写在字母之前;如果是分数与字母相乘,分数要写成假分数的形式,不能写成带分数;如果是商的形式,不要写“÷”号,要写成分数的形式;以及带有单位时的处理方法等等。

列代数式表示数量关系时,首先要读懂题意,然后用正确的书写方式。
例题1:用代数式表示:
(1)比x的平方的5倍少2的数:_____;(2)x的相反数与y的倒数的和:_____;(3)x与y两数的差的平方:_____;(4)某商品的原价是a元,提价10%后的价格:_____;(5)有一个三位数,个位数字比十位数字少4,百位数字是个位数字的2倍,设x表示十位数字,用代数式表示这个三位数:_____;(6)三个连续偶数,中间一个为2n(n为整数)则他们分别为 _____, _____,_____.
分析:(1)先求x的平方,再算5倍,最后减2,注意运算顺序;(2)先求x的相反数和y的倒数,然后将两数相加;(3)先求x与y的差,然后用括号括起来,求这个整体的平方;(4)提价10%后的价格即为原价的1 10%;(5)首先分别用x分别表示各个数位上的数字,再进一步根据数位的意义表示这个数,最后进行整理;(6)根据相邻的两个偶数相差为2进行填空.

注意书写格式,能够化简的要化到最简形式。

例题2:如图所示某长方形广场的四角都有一块半径相同的四分之一圆形的草地.若圆形半径为r米,长方形的长为a米,宽为b米.
(1)请用含a、b和r的代数式表示空地的面积.(2)若长方形长a为300米,宽b为200米,圆形的半径r为10米,求广场空地的面积.(结果保留π)
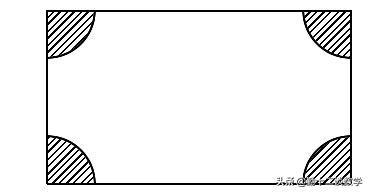
分析:(1)长方形的面积减去一个圆的面积就是空地的面积;(2)把a、b、r的值代入,即可求出答案.
解:(1)空地的面积是(ab-πr^2)平方米;(2)当a=300,b=200,r=10时,广场空地的面积是ab-πr^2=(60000-100π)平方米.
列代数式解决几何问题时,如果涉及到圆,一般周长和面积中的π不用3.14代替。求面积的表达式时,仍然可以使用割补法和转化法,几种平面图形面积的求法不要忘记。

例题3:某超市在“元旦”期间对顾客实行优惠,规定一次性购物优惠办法:少于200元,不予优惠;高于200元但低于500元时,九折优惠;消费500元或超过500元时,其中500元部分给予九折优惠,超过500元部分给予八折优惠.根据优惠条件完成下列任务:
(1)王老师一次性购物600元,他实际付款多少元?
(2)若顾客在该超市一次性购物x元,当x小于500但不小于200时,他实际付款0.9x,当x大于或等于500元时,他实际付款多少元?(用含x的代数式表示)
(3)如果王老师两次购物货款合计820元,第一次购物的货款为a元(200<a<300),用含a的式子表示王老师两次购物实际付款多少元?
分析:(1)让500元部分按9折付款,剩下的100按8折付款即可;(2)等量关系为:500×9折 超过500的购物款×8折;(3)两次购物王老师实际付款=第一次购物款×9折 500×9折 (总购物款-第一次购物款-第二次购物款500)×8折,把相关数值代入即可求解.
解:(1)由题意可得:500×0.9 (600-500)×0.8=530(元),答:他实际付款530元;
(2)由题意可得,他实际付款:500×0.9 (x-500)×0.8=0.8x 50;
(3)由题意可得,老师两次购物实际付款:0.9a 0.8(820-a-500) 450=0.1a 706.

高频考点四:列代数式解决规律探究问题
例题4:观察图1至5中,小黑点的摆放规律,并按这样的规律继续摆放,记第n个图中的小黑点个数为y.解答下列问题:
(1)填表

(2)写出求y的公式(用含n的代数式表示)
(3)当n=50时,小黑点的个数y是多少?
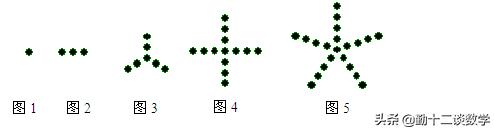
分析:(1)依次数出小黑点的个数即可;(2)依次得到小黑点的个数与图形序号之间的关系即可;(3)把n=50代入(2)得到的关系式即可.






