【考试要求】
1.结合实例,借助几何直观了解函数的单调性与导数的关系;能利用导数研究函数的单调性;对于多项式函数,能求不超过三次的多项式函数的单调区间;
2.借助函数的图象,了解函数在某点取得极值的必要条件和充分条件;
3.能利用导数求某些函数的极大值、极小值以及给定闭区间上不超过三次的多项式函数的最大值、最小值;体会导数与单调性、极值、最大(小)值的关系.
【知识梳理】
1.函数的单调性与导数的关系
函数y=f(x)在某个区间内可导,则:
(1)若f′(x)>0,则f(x)在这个区间内单调递增;
(2)若f′(x)<0,则f(x)在这个区间内单调递减;
(3)若f′(x)=0,则f(x)在这个区间内是常数函数.
2.函数的极值与导数

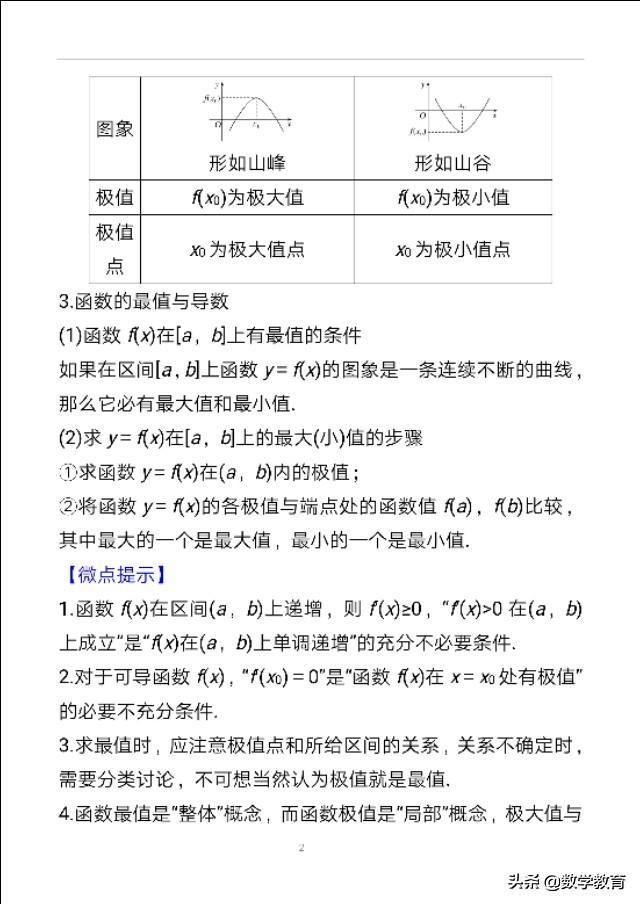




【规律方法】 1.求函数单调区间的步骤:
(1)确定函数f(x)的定义域;(2)求f′(x);(3)在定义域内解不等式f′(x)>0,得单调递增区间;(4)在定义域内解不等式f′(x)<0,得单调递减区间.
2.若所求函数的单调区间不止一个时,用“,”与“和”连接.


1.(1)研究含参数的函数的单调性,要依据参数对不等式解集的影响进行分类讨论.
(2)划分函数的单调区间时,要在函数定义域内讨论,还要确定导数为0的点和函数的间断点.
2.个别导数为0的点不影响所在区间的单调性,如f(x)=x3,f′(x)=3x2≥0(f′(x)=0在x=0时取到),f(x)在R上是增函数.





【规律方法】 1.利用导数比较大小,其关键在于利用题目条件构造辅助函数,把比较大小的问题转化为先利用导数研究函数的单调性,进而根据单调性比较大小.
2.根据函数单调性求参数的一般思路
(1)利用集合间的包含关系处理:y=f(x)在(a,b)上单调,则区间(a,b)是相应单调区间的子集.
(2)f(x)是单调递增的充要条件是对任意的x∈(a,b)都有f′(x)≥0且在(a,b)内的任一非空子区间上,f′(x)不恒为零,应注意此时式子中的等号不能省略,否则漏解.
(3)函数在某个区间存在单调区间可转化为不等式有解问题.

【反思与感悟】
1.已知函数解析式求单调区间,实质上是求f′(x)>0,f′(x)<0的解区间,并注意函数f(x)的定义域.
2.含参函数的单调性要注意分类讨论,通过确定导数的符号判断函数的单调性.
3.已知函数单调性求参数可以利用给定的已知区间和函数单调区间的包含关系或转化为恒成立问题两种思路解决.
【易错防范】
1.求单调区间应遵循定义域优先的原则.
2.注意两种表述“函数f(x)在(a,b)上为减函数”与“函数f(x)的减区间为(a,b)”的区别.
3.在某区间内f′(x)>0(f′(x)<0)是函数f(x)在此区间上为增(减)函数的充分不必要条件.
4.可导函数f(x)在(a,b)上是增(减)函数的充要条件是:对∀x∈(a,b),都有f′(x)≥0(f′(x)≤0),且f′(x)在(a,b)的任何子区间内都不恒为零.

















