本文转载自侨都江门小学初高中全科高效补习,略有修改
高中数学立体几何中线面平行、线面垂直是高考热门考点,也是同学们学习中的一个小难点,本文利用两道例题说明其中的解题特点。
基础知识一、直线与平面平行的判定定理
1、文字语言:如果平面外一条直线和这个平面内的一条直线平行,那么这条直线和这个平面平行。
简记:线线平行,则线面平行。
2、符号语言
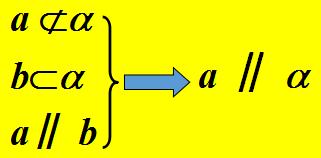
3、图形语言

4、注意
a.定理中三个条件缺一不可;
b.定理告诉我们:要证线面平行,只要在平面内找到一条直线,使线线平行即可。
二、直线与平面垂直的判定定理
图形语言

适用说明
本篇文章一共两道例题,初学者或现阶段成绩在0分-60分的同学重点关注例2;60分-90分的同学重点关注例1。
例一 2017·天津高考

【适用说明】
这道例题适合现阶段成绩在60-90分的同学重点关注
【解析】


例二 2015·福建高考

【适用说明】
这道例题适合初学者或现阶段成绩在0-60分的同学重点关注
【分析】
取AE中点H,连接HG、H的,利用四边形ABCD是矩形得到一组对面平行,可得证。

通过上面两例,我们可以得出立体几何证明线面平行的关键点。
线面平行,关键是找到那条线,无论在平面上还是立体图形中,线线平行直观上都是平行的,线线垂直则不是(立体图形中线线垂直直观上不是90°)。
直接作出那条辅助线,看得到那条线与已知直线的大小长短关系,
若不相等,就构造一个三角形,利用中位线性质(如上例2017·天津高考);
若相等,就构造一个平行四边形,利用对面平行即可(如上例2015·福建高考)。
强化练习2014·北京高考

2017·南山区月考 2012·大纲版

刷题大师为大家精选高中数学学习文章和试题、并提供错题本功能,为大家的学习助力.欢迎点击文章后广告或者本头条号首页底部,下载刷题大师APP进行使用.祝大家学习进步.






