你有没有想过卷积有什么特别之处? 在这篇文章中,我从第一原理中推导出卷积,并表明了它的平移对称性。

某些事物实质上是对其本质的一种支持。 (Claude Adrien Helvetius)
在本科学习期间,我在以色列的Technion参与了电气工程,令人感到震惊的一个重要的概念是,卷积[1]的突如其来。就像一粒沙子落入眼睛里,它扰乱了信号处理世界原本美丽的画面。 让卷积从第一原则中产生,将会多么美好! 正如我将在这篇文章中所展示的,这里的第一原则即平移不变性或对称性。
首先,从基本信号处理课程中教授的公式开始,定义两个n维向量x和w:的离散卷积[2]:
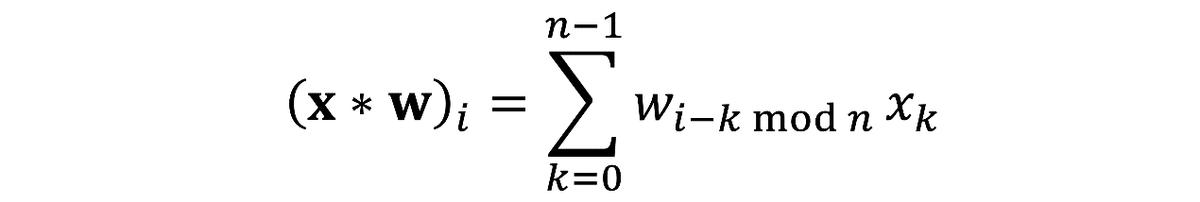
为了方便起见,假设所有的索引从零到n−1,并且是n模,自然而然地想到在圆上定义的向量,把上面的公式写成矩阵向量乘法,得到了一个非常特殊的矩阵,称之为循环(circulant)矩阵:
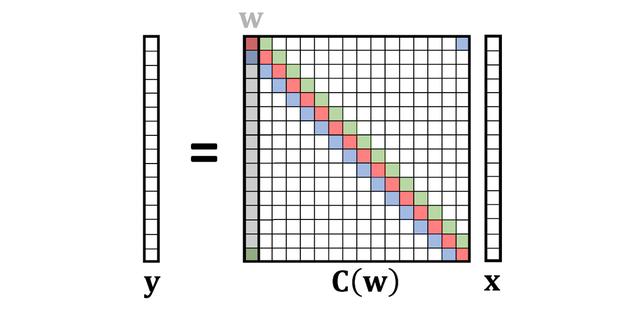
循环矩阵具有多对角结构,每个对角线上的元素具有相同的值。 它可以通过将向量w的移位(模n)叠加在一起来生成[3];因此,用C(W)来表示,指的是由向量w形成的循环矩阵。由于任何卷积x∗w都可以等价地表示为循环矩阵C(W)x的乘法,所以将交替使用这两个术语。
在线性代数中学习的第一件事是矩阵乘法不满足交换率,也就是说,一般情况下,AB≠BA。 然而,循环矩阵是非常特殊的例外:
循环矩阵满足交换律,即:C(w)C(u)=C(u)C(w)。 对于任何循环矩阵,或u和w的任何选择,这都是正确的。同样,可以说卷积是一个满足交换率的运算,x∗w=w∗x。

选择特定的w=[0,1,0…,0]生成一个特殊的循环矩阵,将向量向右移动一位。 这个矩阵叫做(右)移位算子 [4],用S表示。右移位算子的转置是左移位算子。 显然,左移后右移(或反之)不起任何作用,这意味着S是正交矩阵:

循环矩阵满足交换率,它足以表明移位的交换性(在[5]中引理3.1):
当且仅当它移位满足交换率时,称矩阵是循环的。
首先,“当且仅当”是指一种非常重要的性质,即平移或移位等差[6]:卷积与移位的交换性意味着无论我们是先移动向量,然后卷积向量,还是先卷积然后移位,结果都是相同的。

其次,可以将卷积定义为移位等变线性运算:为了使移位符合交换率,矩阵必须具有循环结构。 这正是我们所期望的,从平移对称[7]的第一原理中导出卷积。 而不是给出卷积的公式并证明其移位等差性质,这通常是在信号处理书籍中来推导的,我们可以从移位等差的要求开始,得出卷积的公式,作为满足它的唯一可能的线性运算。

信号处理课程中教授的另一个重要事实是卷积和傅里叶变换[8]之间的联系。 在这里,傅里叶变换从天而降,之后是它对角化卷积操作,在频域中执行两个向量的卷积,作为它们的傅里叶变换的元素乘积。 从来没有人解释过这些正弦和余弦来自哪里,以及它们有什么特别之处。
为了弄清真相,回想一下线性代数中的一个事实:
交换矩阵是联合对角的。
换句话说,满足AB=BA的两个矩阵将具有相同的特征向量(但可能是不同的特征值)[9]。 由于所有循环矩阵都满足交换率,可以选择其中一个并计算其特征向量-上述定理保证了这些矩阵的特征向量也将是所有循环矩阵的特征向量。
由于S是正交矩阵,所以我们期望它的特征向量也是正交的[10]。 一个简单的计算(见[5]第4.1节)得出了这样的结论
移位算子通过傅里叶变换对角化。
在这一点上,可以有今天的第二个“啊哈”时刻:这便是sines和cosines的来源! 它们是移位算子的特征向量;我将它们表示为矩阵Φ的列。 注意特征向量是复杂的,所以在转置Φ时需要采取复共轭。和Φ*进行的乘法(从左)称为傅里叶变换,并通过Φ实现傅里叶逆变换。

由于所有循环矩阵都是对角的,所以它们也由傅里叶变换[11]对角化,只在特征值上有所不同。 最后还要认识到这一点
其中C(w)的特征值为w的傅里叶变换。
现在可以把图中的所有部分导出卷积定理:卷积x∗w可以通过计算原始坐标系统中x(有时称为“空间域”卷积)的循环矩阵C(W)来实现,也可以通过傅里叶(在频域)变换来实现:首先计算Φ*x的傅里叶变换,再将其和w [12]的傅里叶变换相乘之后,计算傅里叶逆变换。
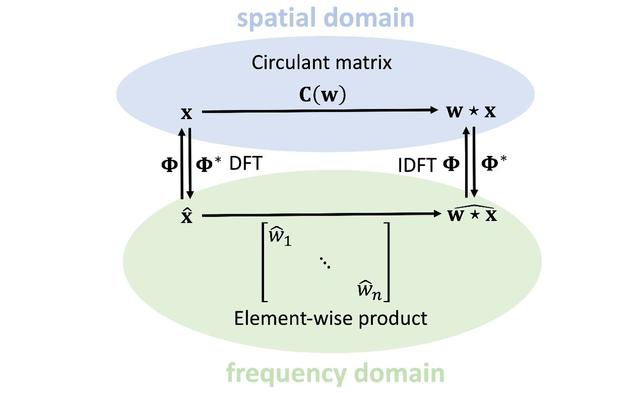
由于Φ具有特殊的冗余结构,Φ*x和Φx的乘积可以用快速傅里叶变换(FFT)算法的复杂度 (n log n)计算。
为什么要这样来定义卷积?在这里我将重复Helvetius的名言:“对某些原则的了解很容易弥补对某些事实的缺乏”。对于卷积而言,它从第一原则的推导更加容易推广到其他领域。
,




