一、向量与三角
前言:向量与三角常考的就是向量与解三角形,向量与三角函数.
①向量与解三角
向量与解三角常考的就是向量的运算及其应用以及向量与解斜三角形.
补充:
1. 向量的运算

向量加法就是根据方向来进行加法运算,向量加法可以将其看做是向量可达路径.

向量减法就是向量加法的逆运算,将向量减法通过改变方向从而改变正负,将向量减法变为向量加法.

向量的数乘运算就是通过向量乘以某个常数之后,进行扩大缩小放大,或者反向。数乘运算之后的向量前面的数正负性决定向量的方向,数的大小决定放大还是缩小。
2. 向量的坐标运算

向量的坐标运算只有加减乘三种运算,并且尤为需要注意的是向量加加减之后仍然为向量,向量的乘法得到的结果是代数,也就是一个值.
3. 斜三角形
按照角形可以分为直角三角形与斜三角形.
按照角度的大小可以分为锐角三角形,直角三角形,钝角三角形.
②向量与三角函数
向量与三角函数常见的考法就是向量的平行、垂直与三角函数,向量的模与三角形函数,向量的数量积与三角函数。
补充:
1. 向量的平行
向量的平行有两种表达形式:
第一种就是用向量表示平行.

第二种就是向量的坐标运算.

2. 向量的垂直
向量的垂直有两种表达形式:
1) 向量表示垂直

2) 向量坐标表示垂直
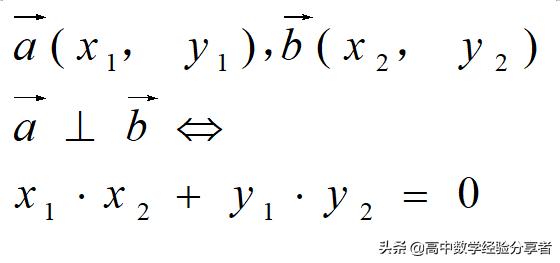
3. 向量的模
向量的模长运算两种方法:
第一种方法就是利用向量的数量积公式.

第二种方法就是利用向量的坐标运算表示.

4. 向量的数量积
向量的数量积公式:






