分数大小比较看似简单,但学生的出错率却很高,为什么呢?细细分析起来,这类大小比较的题目并非简单,它既含有数理的知识,又有方法的灵活运用,对孩子的数感要求非常高。

由于这一部分的学习内容安排在五年级下册《通分》一节,异分母的分数大小比较是通过通分来实现的,通分的知识是学习的重点,比较大小是它的“附带物”。因此,孩子认为只有通分才能比较两分数大小。正是由于这种解题思维的模式化,造成了解题方法的单一化,在遇到难一点的题目时,他们出错也就在所难免了。比如:
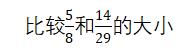
由于通分时的公分母较大,计算复杂,出错的机率就会大大提高。
下面介绍几种比较分数大小的方法,孩子灵活运用这些方法,会大大提高他们作业的正确率,在做题的同时也有效的训练了他们的思维。
第一、基本方法:(1)同分母分数比大小,分子大的那个数大;(2)同分子分数比大小,分母小的那个数就大;(3)异分母分分数比大小,先通分。
第二、基础知识:(1)真分数小于假分数;(2)两个假分数比大小,化成带分数更容易看出大小;(3)分、小数大小比较,化成小数比较简单。(4)数量比大小,要统一单位。

第三、经验数感:(1)折半比较;

(2)分子、分母相差1,分母大的分数值大。

掌握了这些方法还不能保证孩子作业不出错,还要通过大量的练习,将这些方法转化为能力,做到灵活运用。例如:将下面的一组数按从小到大的顺序排列:

第一步,用“折半法”把这六个数分成两组,在组内比出大小,

如要找出更多,只要把它们的分子、分母分别扩大若干倍就行了。例如,分子、分母分别扩大10倍,


掌握知识与方法,强化练习,把知识与方法转化为解题能力才是数学学习的本质。
,




