
图:pixabay
什么是人工神经网络?
现在,我相信我们大家都很熟悉什么是A-NN了,但接下来请允许我按照自己的理解给A-NN下个定义——它是一个强健有力的,同时也非常复杂的机器学习技术,它可以模仿人类的大脑,继而模仿大脑的运作。
正如我们的人脑一样,在一个层次上和神经元网络中有数百万个神经元,这些神经元通过一种称之为synapses(突触)的结构彼此紧紧相连。它可以通过 Axons(轴突),将电信号从一个层传递到另一个层。这就是我们人类学习事物的方式。 每当我们看到、听到、感觉和思考时,一个突触(电脉冲)从层次结构中的一个神经元被发射到另一个神经元,这使我们能够从我们出生的那一天起,就开始学习、记住和回忆我们日常生活中的东西。
好的,接下来我保证大家看到的不再是生物学领域的知识了。
什么是激活函数,它在神经网络模型中是如何使用的?
激活函数(Activation functions)对于人工神经网络模型去学习、理解非常复杂和非线性的函数来说具有十分重要的作用。它们将非线性特性引入到我们的网络中。其主要目的是将A-NN模型中一个节点的输入信号转换成一个输出信号。该输出信号现在被用作堆叠中下一个层的输入。
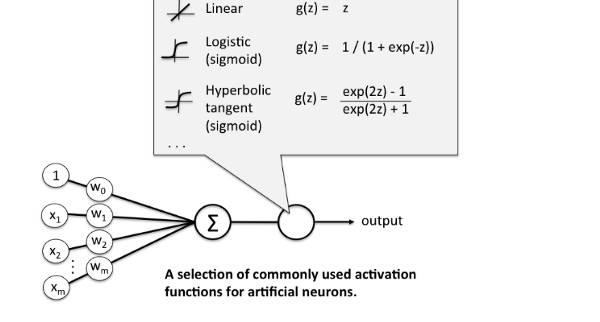
而在A-NN中的具体操作是这样的,我们做输入(X)和它们对应的权重(W)的乘积之和,并将激活函数f(x)应用于其获取该层的输出并将其作为输入馈送到下一个层。
问题是,为什么我们不能在不激活输入信号的情况下完成此操作呢?
如果我们不运用激活函数的话,则输出信号将仅仅是一个简单的线性函数。线性函数一个一级多项式。现如今,线性方程是很容易解决的,但是它们的复杂性有限,并且从数据中学习复杂函数映射的能力更小。一个没有激活函数的神经网络将只不过是一个线性回归模型(Linear regression Model)罢了,它功率有限,并且大多数情况下执行得并不好。我们希望我们的神经网络不仅仅可以学习和计算线性函数,而且还要比这复杂得多。同样是因为没有激活函数,我们的神经网络将无法学习和模拟其他复杂类型的数据,例如图像、视频、音频、语音等。这就是为什么我们要使用人工神经网络技术,诸如深度学习(Deep learning),来理解一些复杂的事情,一些相互之间具有很多隐藏层的非线性问题,而这也可以帮助我们了解复杂的数据。
那么为什么我们需要非线性函数?
非线性函数是那些一级以上的函数,而且当绘制非线性函数时它们具有曲率。现在我们需要一个可以学习和表示几乎任何东西的神经网络模型,以及可以将输入映射到输出的任意复杂函数。神经网络被认为是通用函数近似器(Universal Function Approximators)。这意味着他们可以计算和学习任何函数。几乎我们可以想到的任何过程都可以表示为神经网络中的函数计算。
而这一切都归结于这一点,我们需要应用激活函数f(x),以便使网络更加强大,增加它的能力,使它可以学习复杂的事物,复杂的表单数据,以及表示输入输出之间非线性的复杂的任意函数映射。因此,使用非线性激活函数,我们便能够从输入输出之间生成非线性映射。
激活函数的另一个重要特征是:它应该是可以区分的。我们需要这样做,以便在网络中向后推进以计算相对于权重的误差(丢失)梯度时执行反向优化策略,然后相应地使用梯度下降或任何其他优化技术优化权重以减少误差。
只要永远记住要做:
“输入时间权重,添加偏差和激活函数”
最流行的激活函数类型
1.Sigmoid函数或者Logistic函数
2.Tanh — Hyperbolic tangent(双曲正切函数)
3.ReLu -Rectified linear units(线性修正单元)
Sigmoid激活函数:它是一个f(x)= 1/1 exp(-x)形式的激活函数。它的值区间在0和1之间,是一个S形曲线。它很容易理解和应用,但使其不受欢迎的主要原因是:
·梯度消失问题
·其次,它的输出不是以0为中心。它的梯度更新在不同的方向上且走得太远。 0 <output <1,使优化更加困难。
·Sigmoids函数饱和且kill掉梯度。
·Sigmoids函数收敛缓慢。
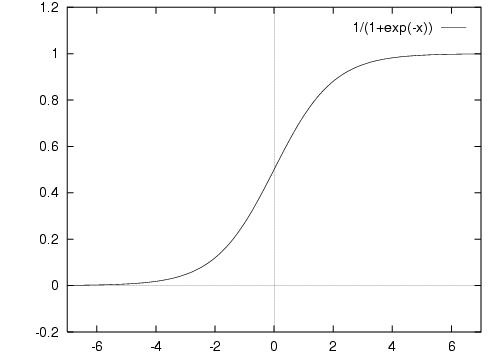
现在我们该如何解决上述问题?
双曲正切函数——Tanh:其数学公式是f(x)= 1 - exp(-2x)/ 1 exp(-2x)。现在它的输出是以0中心的,因为它的值区间在-1到1之间,即-1 <output <1。 因此,在该方法中优化更容易一些,从而其在实践应用中总是优于Sigmoid函数。 但它依然存在着梯度消失问题。

那么我们该如何处理和纠正梯度消失问题呢?
ReLu -Rectified linear units(线性修正单元):其实在过去几年中它就已经非常受欢迎了。最近证明,相较于Tanh函数,它的收敛性提高了6倍。只要R(x)= max(0,x),即如果x <0,R(x)= 0,如果x> = 0,则R(x)= x。因此,只看这个函数的数学形式,我们就可以看到它非常简单、有效。其实很多时候我们都会注意到,在机器学习和计算机科学领域,最简单、相容的技术和方法才是首选,才是表现最好的。因此,它可以避免和纠正梯度消失问题。现如今,几乎所有深度学习模型现在都使用ReLu函数。
但它的局限性在于它只能在神经网络模型的隐藏层中使用。
因此,对于输出层,我们应该使用Softmax函数来处理分类问题从而计算类的概率。而对于回归问题,它只要简单地使用线性函数就可以了。
ReLu函数的另一个问题是,一些梯度在训练过程中可能很脆弱,甚至可能会死亡。它可以导致权重更新,这将使其永远不会在任何数据点上激活。简单地说ReLu可能会导致死亡神经元。
为了解决这个问题,我们引进了另一个被称为Leaky ReLu的修改函数,让它来解决死亡神经元的问题。它引入了一个小斜坡从而保持更新值具有活力。
然后,我们还有另一个变体,它形成于ReLu函数和Leaky ReLu函数的结合,我们称之为Maxout函数。

结论
问题是哪一个更好用呢?
这个问题的答案就是,现在我们应该使用只应用于隐藏层的ReLu函数。当然,如果我们的模型在训练过程中遇到死亡神经元,我们就应该使用leaky ReLu函数或Maxout函数。
而考虑到现实的情况,Sigmoid函数和Tanh函数是不适用的,因为梯度消失问题(vanishing Gradient Problem)是一个很严重的问题,会在训练一个神经网络模型中导致更多问题。
作者:Anish Singh Walia
来源:Medium
,




