前面的文章中介绍了面对中点时可采取的策略,即倍长构造全等(8字型),构造中位线以及构造直角三角形斜边中线。本文仍以两例再加以熟悉。
【例1】如图,在△ABC中,点D,E,F分别是AB,BC,AC的中点,AH是BC边上的高,求证∠DEF=∠DHF.
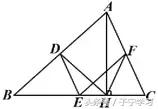
【分析】首先由中位线的性质可得四边形ADEF是平行四边形,其次由直角三角形斜边上的中线性质易知∠FAH=∠AHF,∠DAH=∠DHA,最后利用等式性质得证。

【解答】∵D,E分别是AB,BC的中点
∴DE∥AC
同理,EF∥AB
四边形ADEF是平行四边形
∴∠DEF=∠DAF
∵A在Rt△AHC中,F是AC的中点
∴FH=FA=FC
∴∠1=∠2
同理,∠3=∠4
∴∠1 ∠4=∠2 ∠3
即∠DHF=∠DAF
∴∠DEF=∠DHF
【例2】如图,在平行四边形ABCD中,AD=2AB,F是AD的中点,作CE⊥AB,垂足E在线段AB上,连接CF,EF.
求证:(1)EF=CF;(2)∠EFD=3∠AEF.

【分析】此题的关键是用好中点F以及CE⊥AB这两个条件。那么如何构图才能使这两个条件发挥得淋漓尽致呢?
【简答】延长CF,BA,相交于G点

(1) 易知△AFG≌△DFC
∴GF=FC
即F是GC的中点
又∵△CEG是直角三角形
∴EF=GF=FC

(2) 易知FD=CD
∴∠1=∠2
又∵∠1=∠3,∠3=∠4
∴∠2=∠4
∵∠3 ∠4=∠5
∴∠5=2∠4
∴ ∠EFD=∠5 ∠2=2∠4 ∠4=3∠4
即∠EFD=3∠AEF
解题感悟:
延长中线既构造了8字型全等,又构造了直角三角形斜边中线,一举两得,一箭双雕,妙哉!
见到中点有三法,
一是倍长中线法,
二是斜边中线法,
三是两边中点相连法
,