当分析机械故障类型、故障位置以及故障严重程度时,就需要对滚动轴承的振动信号进行频谱分析,即根据频谱图中的频率成分以及各有关频率成分的幅值大小对滚动轴承进行进一步地诊断。
所谓频域分析,即是把以时间为横坐标的时域信号通过傅里叶变换转为以频率为横坐标的频域信号,从而求得关于原时域信号频率成分的幅值和相位信息的一种分析方法。其数学运算式为

式中 x(t)————时域信号(振动加速度、速度或位移等一切以时间∶为自变量的函数);X(f)——信号的频域表示,是以频率为自变量的函数。
对于周期信号,经过傅里叶变换后得到的幅值谱|X(f)|是离散谱,即构成信号的频率成分是基波及其各次谐波分量。而对于非周期信号,其幅值谱|X(f)|是连续谱,即信号连续地分布在一定的频率范围内。应该指出,通过快速傅里叶变换(FFT)数值计算所得的频谱都是离散谱。
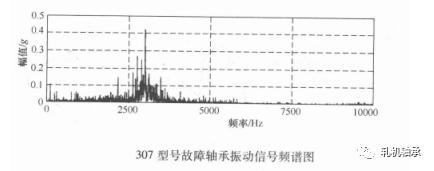
在滚动轴承振动信号分析中,常用到的频域参数有重心频率 FC、均方频率MSF、均方根频率RMSF、频率方差VF、频率标准差RVF等,对于滚动轴承其特征频率峰值也可以作为特征参数诊断故障。由于滚动轴承振动信号中常常含有大量的噪声,直接对振动信号进行频谱分析,故障特征频率成分在频谱图上没有突出显示,为了能够在频谱图上凸显故障特征频率,常常需要对振动信号进行降噪处理,然后再进行频谱分析。时域同步平均法是常用的信号降噪处理方法,它可以提取有用的周期信号,抑制噪声与其他非周期信号。下图为307型号故障轴承振动信号频谱图。
转速约为660r/min 时,正常及几种典型故障的滚动轴承信号的时域波形和频谱图,如下表所示。


从时域波形中可以看出,正常滚动轴承的振动信号基本是平稳的随机波形,当轴承各元件出现不同类型的故障时,其振动幅值有不同程度的增加,波形也有所改变,即出现一些周期性或不规则的冲击、毛刺。同时,从幅值谱中可以发现,正常及各种故障滚动轴承振动信号的能量在频率轴上的分布有着相似性,主要分布在低频段100Hz以下和高频段2000~5000Hz两个区域内。当轴承出现故障时,其各频段的能量有不同程度的增大,能量聚集的中心位置也发生了相应变化。
以上分析说明,试验采集的滚动轴承正常与各种故障信号之间无论时域波形还是幅值谱都存在差异,轴承的故障信息能够在所采集的信号中反映出来。但是由于试验台电机等其他部件振动的影响和信号采集过程不可避免引入的干扰,使滚动轴承的故障信息往往被淹没在强大的背景噪声之中,加上正常轴承与故障轴承信号之间的差异十分微小且不够直观,因此进行简单的时域波形观察和幅值谱分析并不能准确、有效地判定轴承的运行状态、故障部位和故障模式,需要做进一步的分析与处理。
更多精彩内容敬请关注【轧机轴承】公众号
,




