被誉为乐器之王的钢琴,是一种很娇贵、敏感的乐器,在长期使用过程中,任何钢琴都会出现机械故障。
定期的调律维护是必不可少的,钢琴调律师以十二平均律理论为依据,对琴弦的张力和机件的运动进行调整,使所调钢琴的琴音又准又稳。
十二平均律,是一种音乐定律方法, 简而言之,就是把半根琴弦按照等比数列平均分成十二份。

12个数构成等比数列太过复杂,现在我们探讨三个数成等比数列的规律。在两个非零数字a和b之间,插入一个数G,使得a,G,b成等比数列,那么称G是a与b的等比中项。
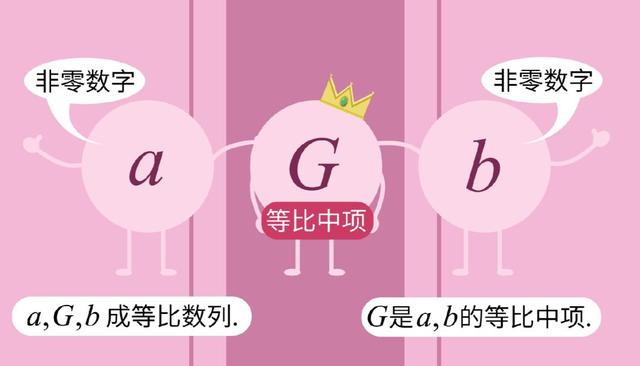
按照等比数列的定义,一定会有G比a,等于b比G。这个式子整理一下,能得到a乘以b,等于G平方,这个乘法式,也就是等比中项公式。

比如12,6,3这三个数,构成一个公比为二分之一的等比数列,那么我们就说6是12和3的等比中项,而且它们一定满足等比中项公式,也就是12乘以3,等于6的平方。
等比数列an中,任意相邻三项an-1,an,an 1,都是成等比数列的,所以一定满足等比中项公式,an-1乘以an 1,等于中间项an的平方。
在等比数列中,中项公式也可以由公比q直观地表现出来, an 1,可以表示为an乘以q, an-1,可以表示为an除以q,这样的话,an-1,与an 1相乘,会恰好等于an的平方,同样的, an 2,可以表示为an乘以q平方, an-2,可以表示为an除以q平方。
那么an-2乘以an 2,也会等于an的平方。以此类推,等比数列中,只要下角标为正整数,由中项公式可以推广得到,an的平方,等于an-1乘以an 1 ,同时也等于an-2乘以an 2,等等,等于到an-k乘以an k 。

例如等比数列an中,a4乘以a6等于2,求a2乘以a8. 我们用等比中项规律来解这个题,a4与a6的中间项是a5,所以满足等比中项公式,a4乘以a6,等于a5平方,
同时,a2与a8,下标2和8的中间数也是5,所以也会满足a2乘以a8,等于a5平方,所以也等于2.
学以致用,用以促学。利用等比中项规律,来解决上面这种问题,会特别方便,大大减少计算量。通过上面这个实例,我们也能发现,等比中项规律的更通用的表现形式,a4乘以a6,等于a2乘以a8。
一般地,等比数列中,只要下标是正整数,am乘以an,等于ap乘以aq,当且仅当,m n,等于p q。 这里要注意,项是乘积相等,而下标是和相等。

这个更一般的等比中项规律,同样也适用于四个数成等比数列的情形。如果四个数a,b,c,d成等比数列,那么一定有ad等于bc成立。
等比中项规律,揭示的是等比数列中的对称性,在具体表现形式上有多种形式,在解题应用时也要灵活挑选。

现在我们利用等比中项公式来求解问题。等比数列an中,a3等于1,a7等于2,求a5. 根据等比中项公式,a5平方等于a3乘以a7,等于1乘以2等于2,所以a5等于正负根号2.
解到这里要注意,因为a5可以表示为a3乘以q平方,所以a5和a3同号。a3等于1为正数,所以a5只能取正根号2. 等比数列中,所有奇数项一定是同号的。
,




