一、基本概念:
1.二次函数的概念:一般地,形如y=ax² bx c(a、b、c是常数且,a≠0)的函数,叫做二次函数。
注意:(1)函数在等号的右边是一个含x的二次整式.
(2)a、b、c为常数,且a≠0,b、c可以为零。当b、c=0时,y=ax²,;当b=0时,y=ax², c;当c=0时,y=ax², bx.
二、基本形式与性质
a 的绝对值越大,抛物线的开口越小。

三、二次函数图象的平移
1. 平移步骤:
⑴ 将抛物线解析式转化成顶点式y=a(x-h)² k,确定其顶点坐标(h,k);
⑵ 保持抛物线y=ax²的形状不变,将其顶点平移到(h,k)处,具体平移方法如下:
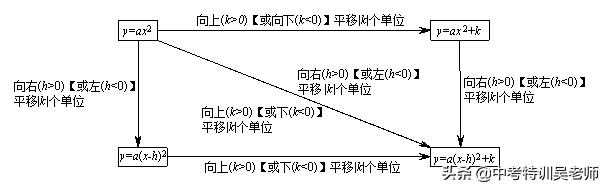
2. 平移规律
在原有函数的基础上概括成八个字“左加右减,上加下减”
四、二次函数解析式的表示方法
1. 一般式:y=ax² bx c(a,b,c为常数,a≠0);
2. 顶点式: y=a(x-h)² k(a,h,k为常数,a≠0);
3. 两根式:y=a(x-x1)(x-x2)(a≠0,x1,x2是抛物线与x轴两交点的横坐标).
注意:任何二次函数的解析式都可以化成一般式或顶点式,但并非所有的二次函数都可以写成交点式,只有抛物线与x轴有交点,即b2-4ac≥0时,抛物线的解析式才可以用交点式表示.二次函数解析式的这三种形式可以互化.
五、二次函数y=ax² bx c图象的画法
五点绘图法:利用配方法将二次函数y=ax2 bx c化为顶点式 y=a(x-h)2 k,确定其开口方向、对称轴及顶点坐标,然后在对称轴两侧,左右对称地描点画图.一般我们选取的五点为:顶点、与y轴的交点(0,c)、以及(0,c)关于对称轴对称的点(2h,c)、与轴的交点(x1,0),(x2,0)(若与x轴没有交点,则取两组关于对称轴对称的点).
画草图时一定要抓住以下几个要点:开口方向,对称轴,顶点,与轴的交点,与轴的交点.
六、二次函数的图象与系数a、b、c之间的关系(中考常考考点)
1. 二次项系数a
二次函数y=ax² bx c中,a作为二次项系数,显然a≠0.
⑴ 当a>0时,抛物线开口向上,a的值越大,开口越小,反之a的值越小,开口越大;
⑵ 当a<0时,抛物线开口向下,a的值越小,开口越小,反之a的值越大,开口越大.
a决定了抛物线开口的大小和方向,a的正负决定开口方向,|a|的大小决定开口的大小.
2. 一次项系数b
在二次项系数a确定的前提下,b决定了抛物线的对称轴.
⑴ 在a>0的前提下,
当b>0时,-b/2a<0,即抛物线的对称轴在y轴左侧;
当b=0时,-b/2a=0,即抛物线的对称轴就是y轴;
当b<0时,-b/2a>0,即抛物线对称轴在y轴的右侧.
⑵ 在a<0的前提下,结论刚好与上述相反,即
当b>0时,-b/2a<0,即抛物线的对称轴在y轴右侧;
当b=0时,-b/2a=0,抛物线的对称轴就是y轴;
当b<0时,-b/2a>0,即抛物线对称轴在y轴的左侧.
在a确定的前提下,b决定了抛物线对称轴的位置.
a、b的符号的判定:对称轴在轴左边则ab>0,在y轴的右侧则ab<0,我们常说的“左同右异”就是这么来的.
3. 常数项c
⑴ 当c>0时,抛物线与y轴的交点在x轴上方,即抛物线与y轴交点的纵坐标为正;
⑵ 当c=0时,抛物线与y轴的交点为坐标原点,即抛物线与y轴交点的纵坐标为0;
⑶ 当c<0时,抛物线与y轴的交点在x轴下方,即抛物线与y轴交点的纵坐标为负.
c决定了抛物线与y轴交点的位置.
只要a、b、c都确定,那么这条抛物线就是唯一确定的.
七、二次函数图象的对称
二次函数图象的对称一般有四种情况,可以用一般式或顶点式表达
1. 关于轴对称
y=ax² bx c关于x轴对称后,得到的解析式是y=-ax²-bx-c;
y=a(x-h)² k关于x轴对称后,得到的解析式是y=-a(x-h)² k;
2. 关于y轴对称
y=ax² bx c关于y轴对称后,得到的解析式是ax²-bx c;
y=a(x-h)² k关于轴对称后,得到的解析式是y=a(x h)² k;
3. 关于原点对称
y=ax² bx c关于原点对称后,得到的解析式是y=-ax² bx-c;
y=a(x-h)² k关于原点对称后,得到的解析式是y=-a(x h)²-k;
4. 关于顶点对称(即:抛物线绕顶点旋转180°)
y=ax² bx c关于顶点对称后,得到的解析式是;
a(x h)² k关于顶点对称后,得到的解析式是y=-a(x-h)² k.
八、二次函数与一元二次方程:
1. 二次函数与一元二次方程的关系(二次函数与x轴交点情况):
一元二次方程ax² bx c=0是二次函数 y=ax² bx c当函数值y=0时的特殊情况.
图象与x轴的交点个数:
① Δ=b²-4ac时,图象与x轴交于两点A(x1,0),B(x2,0)(x1≠x2),其中的x1、x2是一元二次方程ax² bx c=0(a≠0)的两根.这两点间的距离.
② 当Δ=0时,图象与x轴只有一个交点;
③ 当Δ<0时,图象与x轴没有交点.
当a>0时,图象落在x轴的上方,无论x为任何实数,都有y>0;
当a<0时,图象落在x轴的下方,无论x为任何实数,都有y<0.
2. 抛物线y=ax² bx c的图象与y轴一定相交,交点坐标为(0,c);
3. 二次函数常用解题方法总结:
⑴ 求二次函数的图象与轴的交点坐标,需转化为一元二次方程;
⑵ 求二次函数的最大(小)值需要利用配方法将二次函数由一般式转化为顶点式;
⑶ 根据图象的位置判断二次函数y=ax² bx c中a,b,c的符号,或由二次函数中a,b,c的符号判断图象的位置,要学会数形结合;
⑷ 二次函数的图象关于对称轴对称,可利用这一性质,求和已知一点对称的点坐标,或已知与轴的一个交点坐标,可由对称性求出另一个交点坐标.
抛物线与轴有两个交点
二次三项式的值可正、可零、可负
一元二次方程有两个不相等实根
抛物线与轴只有一个交点
二次三项式的值为非负
一元二次方程有两个相等的实数根
抛物线与轴无交点
二次三项式的值恒为正
一元二次方程无实数根.
,




