【导语】
上次北笔给大家分享了资料分析中的平均数问题,很多同学觉得非常实用,还在意犹未尽,今天继续给大家带来几道例题~同学们再次巩固一下吧!
先来梳理一下基本知识点
【知识点】现期平均
1.题型识别:问题时间与材料一致 平均(均/每/单位)。
2.计算公式:平均数=总数/个数=A/B。
3.计算形式:后/前(标准给法)。
(1)人均收入=收入/人数,每亩的产量=产量/亩数,单位面积产量=产量/
面积。
(2)单位: 根据单位确定分子分母,速度: km/h。V=S/T,S 的单位是 km,
T 的单位是 h,速度 km/h。
(3)常识:谁是 1 谁就是分母。
4.速算技巧:截位直除。
5.避坑的方法: 做题的规范性。读问题, 看时间; 判题型, 找数据; 列式子,
先别算;要想快,看选项。
例题展示
2017 年, S 市服务业小微样本企业总体实现营业收入 105.39 亿元, 同比增 长 3.1%,增速比 2016 年回落了 15.7 个百分点。户均实现营业收入 510.63 万元。
【例 11】(2020 四川) 2017 年, S 市服务业小微样本企业共有多少户?
A.不到 3000 户 C.4001~5000 户之间
B.3000~4000 户之间
D.超过 5000 户
【解析】例 11.题目已知收入、户均收入, 列式: 户数=收入/户均收入
=105.39*108/510.63*104 ≈10539/5.1, 首位商 2, 答案为 2000 ,对应A项。【选A
】
【注意】这样的题目一般不会考查量级,不带单位计算的正确率为 99.9%
【知识点】基期平均:
1.题型识别:问题时间在材料之前 平均数问法(均/每/单位)。
2.计算公式: 基期平均=A/B*[(1 b) /(1 a) ]。a: 分子的增长率; b:分
母的增长率。
3.推导: 2021 年总收入为 A,增长率为 a,人数为 B,增长率为 b,2021 年
的人均收入=A/B,问 2020 年收入。 2020 年的人均收入=2020 年总收入/2020 年
人均收入=A/( 1 a)÷ [B/( 1 b) ]=A/B*[( 1 b) /( 1 a) ]。
4.速算技巧:
(1)先截位直除 A/B。
(2)再看( 1 b) /( 1 a)与 1 的关系(>,<, =),结合选项选答案。
2017 年民办初中 5277 所, 比上年增长 3.78%; 在校生 577.68 万人, 比上年 增长 8.42%。民办普通高中 3002 所,比上年增长 7.71%;在校生 306.26 万人, 比上年增长 9.74%。民办中等职业学校 2069 所,比上年下降 2.17%;在校生 197.33 万人,比上年增长 7.16%。
【例 12】(2020 北京) 2016 年平均每所民办中等职业学校在校生人数约为
A.871 人
C.1091 人
B.991 人
D.1181 人
【解析】例 12.时间给 2017 年, 问 2016 年, 时间为基期, 出现“平均每所”,
基 期 平 均 数 问 题 , 平 均 数 = 人 数 / 所 数=A/B 。 公 式 : A/B*[ ( 1 b ) /
(1 a) ]=197.33/2069*[(1-2.17%) /(1 7.16%) ], 列式的时候 A 和 a 一起列
出来, B 和b 一起列出来。 C、D 项首位相同, 次位差等于首位, 截三位计算, 用
197.33/207, 首位商 9, 次位商 5,(1-2.17%) /(1 7.16%)< 1,950*1-<950,
对应 A 项。【选 A】
2017 年 1~12 月, 全国内燃机累计销量 5645.38 万台, 同比增长 4.11%,累 计完成功率 266879.47 万千瓦, 同比增长 9.15%, 其中柴油内燃机功率同比增长 34%。
【例 13】(2019 浙江) 2016 年,我国销售的内燃机平均功率约为:
A.35 千瓦 B.45 千瓦
C.55 千瓦 D.65 千瓦
【解析】例 13.时间给 2017 年问 2016 年, 求基期, 已知销量和功率, 平均
功率=功率/销量, 列式: A/B*[( 1 b)/( 1 a)]=266879.47/5645.38*[( 1 4.11%)
/( 1 9.15%)],( 1 4.11%)/( 1 9.15%)< 1,选项差距大,截两位计算, 266879.47/56,
首位商 4, 次位商 7,原式转化为 47*1-,排除 C、D 项。( 1 4.11%) /(1 9.15%)
比 1 小一点, 用钱来比较, 104 元比 109 元小一点,排除 A 项, 对应 B 项。【选
B】
【知识点】两期平均比较——升降:
1.题型识别:题干中涉及两个时间 平均数问法。
2.公式: 现期平均- 基期平均=A/B-A/B*[(1 b) /(1 a) ]=A/B*[(a-b) /
(1 a) ]。A/B>0,1 a>0,比较的时候只比较 a-b。
3.升降判断:
(1) a>b,平均数上升。
(2) a<b,平均数下降。
(3) a=b,平均数不变。
(4) a: 分子的增长率; b: 分母的增长率, a 和b 是率, 带着正负号比较。

【例 14】(2019 国考)能够从上述资料中推出的是:
A.略
B.2017 年 11 月,全国平均每吨进口药品单价低于上年同期水平 C.略
D.略
【解析】例 14.今年和去年比较, 低于上年, 即a<b。时间是 2017 年 11 月,
金额对应 A、a,数量对应 B、b,a=11.9%<b=21.5%,低于上年,正确。【选 B】
【知识点】两期平均比较——平均数的增长量 (单位)。
1.题型识别:题干中涉及两个时间 平均数 增长 具体单位。
2.公式: 现期平均- 基期平均=A/B-A/B*[(1 b) /(1 a) ]=A/B*[(a-b) /
(1 a) ]。有竞争力的题目, 多步除法, 分子分母都截位, 约分、看选项的过程。
3.速算技巧:根据选项估算即可。
2019 年,全国商品房销售面积 171558 万平方米,比上年下降 0.1%。其中,
住宅销售面积增长 1.5%, 办公楼销售面积下降 14.7%, 商业营业用房销售面积下 降 15.0%。商品房销售额 159725 亿元,增长 6.5%,增速比上年回落 5.7 个百分 点。
【例 15】(2020 湖南)与 2018 年相比, 2019 年全国商品房销售均价约:
A.增长 580 元
C.下降 580 元
B.增长 710 元
D.下降 710 元
【解析】例 15.时间 2019 年和 2018 年,选项是增长 多少元,为增长量,
求销售均价的增长量, 判定为平均数增长量问题。均价=商品房销售额/销售面积,
公式: A/B-A/B*[(1 b) /(1 a) ]=A/B*[(a-b) /(1 a) ],a=6.5%,b=-0.1%,
a>b,或着根据常识,房价是上升的,排除 C、D 项。 首位不同,选项差距大,
截两位, 原式≈16/17*66/11=1-*6,选择 A 项。【选 A】
【知识点】平均数的增长率:
1.识别:平均数 增长 %。
2.例子: 2017 年小明家总收入 A, 同比增长率 a; 总人口 B, 同比增长率 b,
求 2017 年小明家人均收入同比增长了 %?
推导:现期 2017 年的平均数=A/B;基期 2016 年的平均数=A/B*[( 1 b) /
(1 a) ]。r= (现期平均-基期平均) /基期平均={A/B-A/B*[(1 b) /(1 a) ]}
÷ {A/B*[(1 b) /(1 a) ]}=[1-(1 b) /(1 a) ]÷ [(1 b) /(1 a) ]=(a-b)
/( 1 b)。
3.公式: r=(a-b) /( 1 b)(a 是分子的增长率; b 是分母的增长率)。
4.做题逻辑:
(1)确定分子、分母(谁/谁)。
(2)代入公式: r=(a-b) /( 1 b)。
(3) 速算方法: 确定分子分母,不要写公式, 分子 a-b 口算,分母写成 1
或者 1- 的形式,最后瞪出选项。
形式一:给 a 和b
2014 年某区限额以上第三产业单位共 674 家, 实际收入 1059.1 亿元, 同比
增长 4.5%; 实现利润总额 13.5 亿元, 同比增长 11.9%; 从业人员达到 58631 人, 同比下降 4.3%。
【例 16】(2019 北京) 2014 年该区限额以上第三产业单位平均每名从业人
员创造的利润比上年约: A.下降了 7%
C.上升了 7%
B.下降了 17%
D.上升了 17%
【解析】例 16.上升/下降 %, 是增长率, 平均数的增长率问题, 公式: r=
(a-b) /( 1 b),确定分子分母,利润增长率 a=11.9%,人数增长率 b=-4.3%,
a>b,为上升, 排除 A、B 项。分子 a-b 口算, 11.9%-(-4.3%) =16.2%,r=16.2%/1-
>16.2%,选择 D 项。【选 D】
2017 年, A 省完成客运总量 148339 万人次, 同比增长 5.4%, 增幅比前三季 度提高 0.2 个百分点, 比上年提高 0.5 个百分点; 完成旅客周转总量 4143.84 亿 人公里,增长 7.7%,增幅比前三季度提高 0.7 个百分点,比上年提高 1.8 个百 分点。
【例 17】(2019 国考) 2017 年前三季度, A 省平均每人次客运旅客运输距离 (旅客周转量/客运总量)同比:
A.下降了不到 2%
C.上升了不到 2%
B.下降了 2%以上
D.上升了 2%以上
【解析】例 17.已知全年, 求前三季度, 上升/下降 %, 平均数增长率问题。
旅客周转量是 A,a=7.7%-0.7%=7%; 客运总量是 B,b=5.4%-0.2%=5.2%,分子 a-
b 口算, r=1.8%/1 ,a>b,上升,排除 A、B 项,一定不到 2%,对应 C 项。【选
C】

【例 18】(2020 国考) 2018 年中国平均每块集成电路出口单价比上年:
A.下降了 30%以上
C.下降了 30%以内
B.上升了 30%以上
D.上升了 30%以内
【解析】例 18.给进口和出口的数量和金额, 平均数问题, 平均数=出口额/
出口量=A/B, 没有 a 和 b, 用“(2018 年平均-2017 年平均) /2017 年平均”计算,
列式:(846.4/2171.0-668.8/2043.5)÷(668.8/2043.5), 看到式子不想计算。
公式: r=(a-b) /(1 b), a≈180/668.8<30%,b≈130/2043.5≈6.5%, 代入数
据: 23.5%/(1 6.5%)>0, 排除 A、C 项; 答案一定小于 23.5%, 选择 D 项。【选
D】
【注意】充分利用 30%,a≈180/668.8<30%, 很接近 30%,b=10-%,则 r=(<
30%) /1 ,答案在 30%以内,选择 D 项。

【例 19】(2020 国考) 2007~2018 年间,全国茶园面积首次超过 200 万公 顷的年份,当年茶园单位面积茶叶产量比上年:
A.下降了 10%以上
C.增加了 10%以上
B.下降了不到 10%
D.增加了不到 10%
【解析】例 19.指 A 打 B 型。先找首次找超过 200 万公顷的年份, 为 2011
年, 问 2011 年单位面积产量, 平均数问题, 上升、下降*%, 平均数增长率问题。
已知产量为 A, 面积为 B, 没有给 a 和 b,a=(160.8-146.3) /143.3≈14/146<
10%; b=(205.6-193.2) /193.2≈12/193≈6%,a>b,排除 A、B 项, r= (<<
10%) /1 ,对应 D 项。【选 D】
【知识点】间隔平均数增长率:时间为间隔, r=(a 间-b 间)/( 1 b 间)。
2017 年, S 市服务业小微样本企业总体实现营业收入 105.39 亿元, 同比增 长 3.1%,增速比 2016 年回落了 15.7 个百分点。
2017 年, S 市服务业小微样本企业总体资产 938.58 亿元,同比增长 4.2%, 增速比 2016 年下降 0.9 个百分点。
【例 20】(2020 四川) 2017 年, S 市服务业小微样本企业平均每万元资产实 现营业收入比 2015 年:
A.增长了不到 5%
C.下降了不到 5%
B.增长了 5%以上
D.下降了 5%以上
【解析】例 20. “平均每万元资产”, 平均数问题, 问 2017 年比 2015 年, 时
间为间隔, 间隔平均数增长率问题, 每万元收入=收入/资产=A/B,可以消掉单位。
公式: r=(a 间-b 间)/(1 b 间)。“2017 年, S 市服务业小微样本企业总体实现营
业收入 105.39 亿元,同比增长 3.1%,增速比 2016 年回落了 15.7 个百分点”,
则 r1=3.1%,r2=3.1% 15.7%=18.8%,a 间=3.1% 18.8% 3.1%*18.8%>20%;“2017
年, S 市服务业小微样本企业总体资产 938.58 亿元, 同比增长 4.2%, 增速比 20
16 年下降 0.9 个百分点”, r1=4.2%,r2=4.2% 0.9%=5.1%,b 间=4.2% 5.1% 4.2%*
5.1%< 10%,a 间>b 间,排除 C、D 项;代入公式, a-b> 10%,r=10 %/1 >5%,对
应 B 项。【选 B】
【知识点】平均数增长率,特殊值: b=0。
1.推导: 平均数增长率公式: r=(a-b) /(1 b), 如果 b=0, 此时 r=(a-0)
/( 1 0) =a/1=a。
2.结论:当分母的增长率 b=0 时,平均数的增长率 r=a 分子的增长率。 b≈
0,平均数 r≈a。
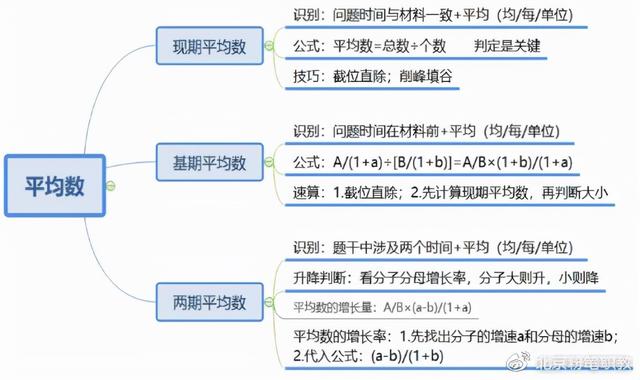
【注意】平均数:
1.现期平均数:
(1)识别:问题时间与材料时间一致 平均(均/每/单位)。
(2)公式:平均数=总数/个数,判定量是关键。
(3)技巧:截位直除;削峰填谷。
2.基期平均数:
(1)识别:问题时间在材料前 平均(均/每/单位)。
(2)公式: A/( 1 a)÷B/( 1 b) =A/B*[( 1 b) /( 1 a) ]。
(3)速算:
①截位直除。
②先计算现期平均数,再判断大小。
3.两期平均数:
(1)识别:题干涉及两个时间 平均(均/每/单位)。
(2)升降判断:看分子分母增长率,分子大则升,小则降。
(3)平均数的增长量: A/B*[(a-b) /( 1 a) ]。
(4)平均数的增长率:
①先找出分子的增速 a 和分母的增速b。
②代入公式:(a-b) /( 1 b)。
,




