点击右上角关注“陈老师初中数理化”分享学习经验,一起畅游快乐的学习生活。
利用正方形的性质求动点的运动轨迹是初二数学的重要题型,本文就例题详细解析这类题型的解题方法,希望能给初二学生的数学学习带来帮助。
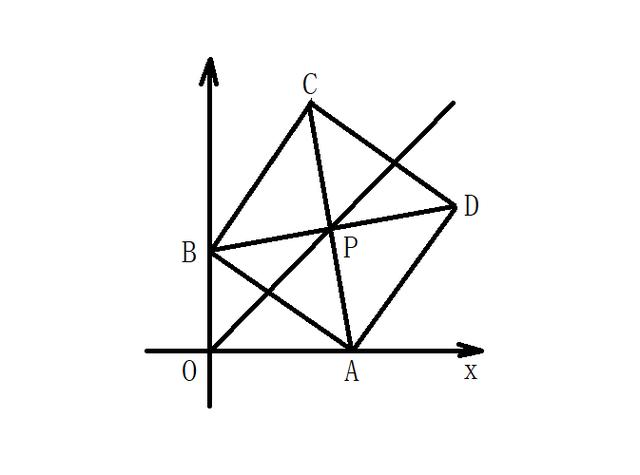
例题如图,在平面直角坐标系中,边长为a(a为大于0的常数)的正方形ABCD的对角线AC,BD交于点P,顶点A在x轴正半轴上运动,顶点B在y轴正半轴上运动(x轴的正半轴,y轴的正半轴都不包含原点O),顶点C,D在第一象限
(1)当∠BAO=45°时,求点P的坐标;
(2)求证:无论点A在x轴正半轴上、点B在y轴正半轴上怎样运动,点P都在∠AOB的平分线上。
解题过程:
1、当∠BAO=45°时,求点P的坐标

根据正方形的性质和题目中的条件:四边形ABCD为正方形,则AC平分∠BAD,∠BAD=90°,AC⊥BD,AP=BP;
根据结论:AC平分∠BAD,∠BAD=90°,则∠BAC=∠BAD/2=45°;
根据题目中的条件和结论:∠BAO=45°,∠BAC=45°,则∠OAP=∠BAC ∠BAO=90°,即AC⊥x轴;
根据平行线的判定和结论:AC⊥BD,AC⊥x轴,则BD∥x轴;
根据平行线的性质和结论:BD∥x轴,∠AOB=90°,则∠DBO ∠AOB=180°,即∠DBO=90°,BP⊥y轴;
根据勾股定理和结论:AB=a,BP=AP,AB^2=AP^2 BP^2,则AP=BP=√2/2a;
根据结论:AP=BP=√2/2a,BP⊥y轴,AC⊥x轴,则点P的坐标为(√2/2a,√2/2a);
2、证明:点P都在∠AOB的平分线上
过点P作PE⊥x轴,PF⊥y轴

根据题目中的条件:PE⊥x轴,PF⊥y轴,AC⊥BD,则∠PEA=∠PFB=∠PEO=∠APB=90°;
根据结论:∠PFB=∠PEO=90°,∠AOB=90°,则∠FPE=90°;
根据结论:∠FPE=∠APB=90°,∠FPE=∠BPE ∠BPF,∠APB=∠BPE ∠APE,则∠BPF=∠APE;
根据全等三角形的判定和结论:∠BPF=∠APE,∠PFB=∠PEA,BP=AP,则△BFP≌△AEP;
根据全等三角形的性质和结论:△BFP≌△AEP,则PE=PF;
根据角平分线的判定和结论:PE⊥x轴,PF⊥y轴,PE=PF,则点P在∠AOB的平分线上。
结语解决本题的关键是利用正方形的性质得到线段、角度间的数量关系,通过构造全等三角形得到线段间的等量关系,进而证明到题目需要的结论。
,




