打开《运筹学》课本,第一章教的便是求解线性规划问题最有效的算法——单纯形法。
自此,任何看似很复杂的问题只要转变成线性规划问题,便能高效求解,发好期刊。
可实际在科研建模时,目标函数或是约束条件,极大概率会出现非线性的形式。
此时若选择采用启发式算法求解,就相当于放弃了求精确解,也放弃了投好期刊。
因此,了解并懂得何种形式可以转化为线性和如何转化,是非常重要的。
总的来说,具有:
分段函数形式、
绝对值函数形式、
最小/大值函数形式、
逻辑或形式、
含有0-1变量的乘积形式、
混合整数形式
以及分式目标函数,均可实现线性化。
线性化的主要手段其实就两点,一点是引入0-1变量,另一点是引入很大的整数M。
灵活运用这两点会呈现非常巧妙且神奇的线性化技巧,希望你也能感受到其中的数学之美。
鉴于以上内容较多,故分两期进行阐述,本期先阐述较为简单的几种。
1.分段函数
若一种产品的采购有固定成本K,那么其采购成本应分为不采购和采购两段:

其线性化方法简单且巧妙:(分类讨论y=0和y=1即可理解)
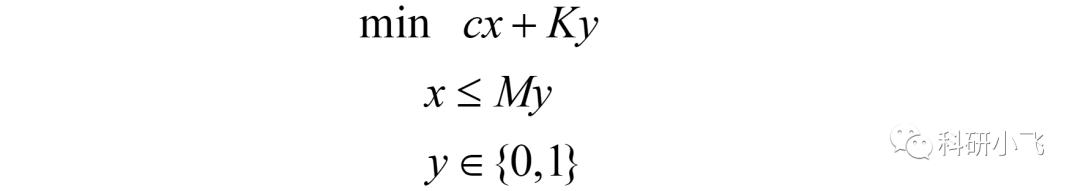
其中,y是引入的辅助0-1变量,M是一个很大的整数。
注:如果当x=0时,成本不是0而是a。此时的分段函数形式也是可以线性化的,聪明的你知道如何转化吗?如果没想到办法,欢迎私信交流。
2.绝对值函数
要求线性化如下数学模型:

方法1:用yi代替绝对值部分

方法2:用ui、vi代替
高中或是高数课上学过如下定理:
定理:

则之前数学模型可以线性化为:

3.MaxMin/MinMax函数
以下图的MaxMin函数为例,基于k 项min CX(矩阵写法省略了求和号,打不了转置符号,望大家理解)函数的值,再取其中的最大值。
该形式下的线性化方法是:用z 替代min CX函数,这样z 便 ≤ CX,又由目标函数是取最大的z,从而限制住z 不会取到0,而只会取满足条件的z。MinMax函数同理。

此时数学感觉良好的同学可能已经意识到这类似于高数课上的夹逼定理(判断极限是否存在),进一步也可能意识到,如果换为MaxMax和MinMin函数,以上这套思路就行不通了。
实际也确实是这样,线性化MaxMax和MinMin函数较为复杂一些,需要借助下面第四点线性化逻辑或的思维。
4.逻辑或
该部分主要针对约束条件(含有逻辑或)的线性化操作。通常,逻辑或两端的约束存在三种情形。
情形1:逻辑或两段均为≤,即:

此时线性化方法为:

引入u 和v 两个0-1变量和大M。分类讨论u 和v 取0或1的四种情形便能理解以上过程。思路非常巧妙,希望大家多悟几遍并消化。
情形2:一端为≤,一端为=,即:

此时线性化方法为:

可见,多添加一个≥的式子即可。那么,情形3如何处理相信大家也猜到了。
情形3:两端均为=,即:

此时线性化方法为:

5.MaxMax/MinMin函数
该部分综合运用了前述技巧。 以MaxMax函数为例:

首先,令z =max CX,但若此时约束条件写成z ≥ CX的形式是不行的,因为这样会让z 取值到无穷大,故一定要写出“z ≤ 某个值”的形式。
这时,就需要引入0-1变量和大M,如上图所示。大家领悟一下。
而yk求和≥1的含义是“至少有一个成立”。实际计算时,只会有一个k 让yk=1,其余yk为0。具体原因,也是夹逼定理的思想,大家多多领会。
同理,MinMin函数的线性化过程如下。

注意,这里是加号。yk=0该约束不起作用,只有当yk=1时才会起作用。
后记
篇幅有限,Max/Min函数、含有0-1变量的乘积形式、混合整数形式以及分式目标函数的线性化操作留在下一期讲。
总的来说,在遇到非线性问题时,建议大家多多尝试引入0-1变量和大M的方法。至于构造时是采用≥还是≤,是加还是减的形式(指± M(1 ± y),是需要自己多多尝试的。
最后,祝大家都能通过线性化技巧发表高水平期刊,祝疫情早日结束。
不闻不若闻之,闻之不若见之;
见之不若知之,知之不若行之。
我是科研小飞,期待您的关注。
欢迎微信搜索“科研小飞”,获取第一手科研分享文章。
,




