
题目:
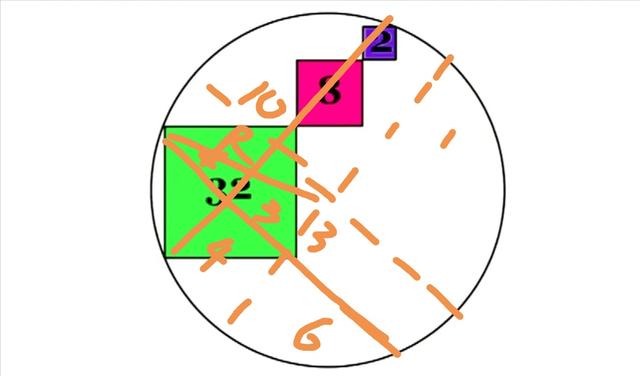
圆中有三个正方形,它们的面积分别为2、8、32,求圆的面积
知识点回顾:
共圆性质定理- 圆内接四边形的对角和为180°,并且任何一个外角都等于它的内对角。
- 四边形ABCD内接于圆O,延长AB和DC交至E,过点E作圆O的切线EF,AC、BD交于P,则有:
- ∠A ∠C=180°,∠B ∠D=180°(即图中∠DAB ∠DCB=180°, ∠ABC ∠ADC=180°)
- ∠DBC=∠DAC(同弧所对的圆周角相等)。
- ∠ADE=∠CBE(外角等于内对角,可通过(1)、(2)得到)
- △ABP∽△DCP(两三角形三个内角对应相等,可由(2)得到)
- AP*CP=BP*DP(相交弦定理)
- EB*EA=EC*ED(割线定理)
- EF²= EB*EA=EC*ED(切割线定理)
- AB*CD AD*CB=AC*BD(托勒密定理)
垂直于弦的直径平分这条弦,并且平分弦所对的两条弧。
正方形性质定理- 两组对边分别平行;四条边都相等;邻边互相垂直。
- 四个角都是90°,内角和为360°。
- 对角线互相垂直;对角线相等且互相平分;每条对角线平分一组对角。
- 既是中心对称图形,又是轴对称图形(有四条对称轴)。
- 正方形的一条对角线把正方形分成两个全等的等腰直角三角形,对角线与边的夹角是45°;正方形的两条对角线把正方形分成四个全等的等腰直角三角形。
- 正方形具有平行四边形、菱形、矩形的一切性质与特性。
- 正方形是特殊的矩形,正方形是特殊的菱形。
粉丝解法1:
两垂直弦长可求,分别向上和向右平移3个单位(14÷2-4=3),即相交于圆心。R²=3² (3 4)²=58s=丌R²=58丌
粉丝解法2:

粉丝解法3:
设圆的半径为R,AB=4根号2,BC=根号{(3根号2)(3根号2) (7根号2)(7根号2)}=2根号29,AC=8 4 2=14,三角形ABC面积=4根号2*7根号2/2=28=14*4根号2*2根号29/4R,R=根号58,圆的面积=3.14*58=128.12。
粉丝解法4:
如图所示:AB=4√2,BC=√【(3√2)^2+(7√2)^2】=2√29,AC=8+4+2=14,s△ABC=1/2x4√2x7√2=28=14x4√2x2√29/4R,R=√58,s圆=58丌。

粉丝解法5:

粉丝解法6:






