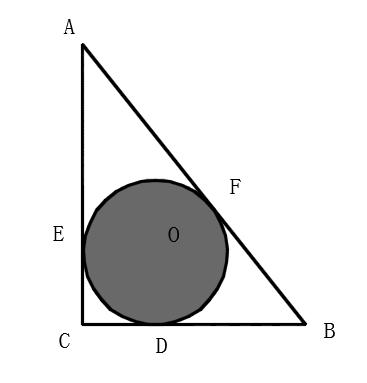
上图,三角形ABC中,角C=90°,AC=b,BC=a,AB=c,则内切圆的半径r=(a b-c)/2
怎么证明?
小写的a,b,c一般我们约定俗成,代表的是顶点字母所对的三角形的边,这个东西首先不能忘?
然后这里是个直角三角形,内切圆的圆形为O,E,D,F都为切点,那么四边形EODC为正方形易知,并且正方形的边长=2r
然后有个三角形通用的等量转换考了无数次了:角平分线与内切圆切点边长的关系,转化到三角形的周长上会是什么情况?
AE=AF, BF=BD等等,
a b-c=BC AC-AB=r BD r AE-AF-BF=r BD r AE-BD-AE=2r
后面略
,