一.比例线段
1、比例线段的相关概念
比例线段:如果选用同一长度单位量的两条线段a,b的长度分别为m,n,那么就说这两条线段的比是a:b=m:n.在两条线段的比a:b中,a叫做比的前项,b叫做比的后项。在四条线段中,如果其中两条线段的比等于另外两条线段的比,那么这四条线段叫做成比例线段,简称比例线段.
若四条a,b,c,d满足a/b=c/d或a:b=c:d,那么a,b,c,d叫做组成比例的项,线段a,d叫做比例外项,线段b,c叫做比例内项,线段的d叫做a,b,c的第四比例项。
注意:线段的单位要统一.
比例中项:如果作为比例内项的是两条相同的线段,即a/b=c/d或a:b=b:c,那么线段b叫做线段a,c的比例中项。

例1.下列四条线段中,能成比例线段的是 ( )
A.a=1,b=1,c=2,d=3
B.a=1,b=2,c=3,d=4
C.a=2,b=2,c=3,d=3
D.a=2,b=3,c=4,d=5
例2.若a∶b=3∶4,且a b=14,则2a-b的值是( )
A.4 B.2 C.20 D.14
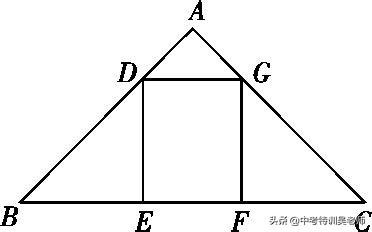
例3.如图,矩形纸片ABCD中,AB>AD,E,F分别是AB,DC的中点,将矩形ABCD沿EF所在直线对折,若得到的两个小矩形都和矩形ABCD相似,则AB与AD的数量关系为 .

2、黄金分割:把线段AB分成两条线段AC,BC(AC>BC),并且使AC是AB和BC的比例中项,即AC/BC=AB/AC或AC²=AB×BC,叫做把线段AB黄金分割,点C叫做线段AB的黄金分割点,其中AC=(√5-1)/2AB≈0.618AB
注意:(1)线段的黄金分割点有两个;
(2)黄金分割的几何作图.
3、比例的性质

二.平行线分线段成比例定理
三条平行线截两条直线,所得的对应线段成比例。由l3∥l4∥l5,得.
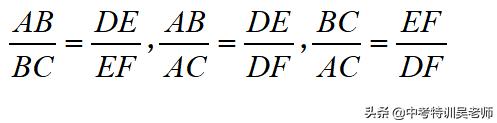

推论:
(1)平行于三角形一边的直线截其他两边(或两边的延长线),所得的对应线段成比例。
逆定理:如果一条直线截三角形的两边(或两边的延长线)所得的对应线段成比例,那么这条直线平行于三角形的第三边。
(2)平行于三角形一边且和其他两边相交的直线截得的三角形的三边与原三角形的三边对应成比例。
例4.如图27-2-1-2,l1∥l2∥l3,直线a、b与l1、l2、l3分别相交于点A、B、C和点D、E、F.若AB=3,DE=2,BC=6,则EF= .


三.相似三角形
1、相似三角形的概念
对应角相等,对应边成比例的三角形叫做相似三角形。相似用符号“∽”来表示,读作“相似于”。相似三角形对应边的比叫做相似比(或相似系数)。
2、相似三角形的基本定理
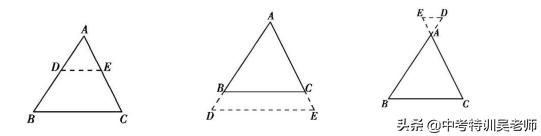
平行于三角形一边的直线和其他两边(或两边的延长线)相交,所构成的三角形与原三角形相似。

用数学语言表述如下:
∵DE∥BC,∴△ADE∽△ABC
相似三角形的等价关系:
(1)反身性:对于任一△ABC,都有△ABC∽△ABC;
(2)对称性:若△ABC∽△A′B′C′,则△A′B′C′∽△ABC
(3)传递性:若△ABC∽△A′B′C′,并且△A′B′C′∽△A″B″C″,则△ABC∽△A″B″C″。
四.三角形相似的判定
1、三角形相似的判定方法
①定义法:对应角相等,对应边成比例的两个三角形相似
②平行法(A型或X型):平行于三角形一边的直线和其他两边(或两边的延长线)相交,所构成的三角形与原三角形相似.
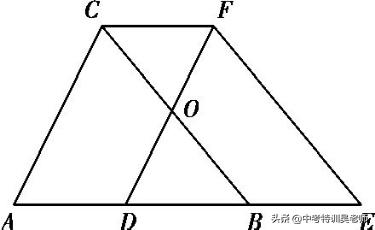
例5.将△ABC沿AB向右平移得到△DEF,DF交BC于点O,连接CF,则图中相似三角形的对数为 ( )
A.3 B.5 C.6 D.7
③两角定理:如果一个三角形的两个角与另一个三角形的两个角对应相等,那么这两个三角形相似,两角对应相等,两三角形相似.

归纳总结:用两角分别相等来判定三角形相似是常用方法,应掌握好寻找等角的方法,同时要注意图形中隐含的等角条件,如公共角、对顶角等.
例6.正方形ABCD中,点E,F,G分别在AB,BC,CD上,且∠EFG=90°.求证:△EBF∽△FCG.

④两边夹角定理:如果一个三角形的两条边和另一个三角形的两条边对应成比例,并且夹角相等,那么这两个三角形相似,两边对应成比例且夹角相等,两三角形相似.

特别提醒:利用该判定定理时,相等的角必须是已知两组成比例边的夹角,否则两个三角形不一定相似.
例7.如图27-2-1-5,已知:∠BAC=∠EAD,AB=20.4,AC=48,AE=17,AD=40.
求证:△ABC∽△AED.

⑤三边定理:如果一个三角形的三条边与另一个三角形的三条边对应成比例,那么这两个三角形相似,三边对应成比例,两三角形相似.

方法技巧:判断两个三角形的三边是否成比例的一般步骤:
(1) 排:将三角形的边按大小顺序排列;
(2)算:分别计算三边的比;
(3)判:由比是否相等来判断两个三角形的三边是否成比例
例8.在平面直角坐标系中,△ABC各顶点的坐标分别是A(1,2),B(1,1),C(2,0),△DEF各顶点的坐标分别是D(-1,6),E(-1,4),F(-3,2),△ABC与△DEF相似吗?请说明理由.

2、直角三角形相似的判定方法
(1)以上各种判定方法均适用
(2)定理:如果一个直角三角形的斜边和一条直角边与另一个直角三角形的斜边和一条直角边对应成比例,那么这两个直角三角形相似.

方法总结:两个直角三角形除去直角外,具备下列条件都可以判定相似:①一个锐角相等;②任意两边成比例.
例9.在Rt△ABC和Rt△DEF中,∠C=∠F=90°,下列条件中不能判定这两个
三角形相似的是 ( )
A.∠A=55°,∠D=35°
B.AC=9,BC=12,DF=6,EF=8
C.AC=3,BC=4,DF=6,DE=8
D.AB=10,BC=6,DE=15,EF=9
③垂直法:直角三角形被斜边上的高分成的两个直角三角形与原三角形相似。
易错点:误认为两边成比例且有一组角相等的两个三角形相似.
在判定两个三角形相似时,若两个三角形具备两边成比例且有一组角相等,要注意相等的这组角必须是夹角(直角三角形除外),不能误认为任意一组角相等即可.

题型一、相似三角形与圆的综合应用
例10.如图,点D在以AB为直径的☉O上,AD平分∠BAC,DC⊥AC,过点B作☉O的切线交AD的延长线于点E.
(1)求证:直线CD是☉O的切线;
(2)求证:CD·BE=AD·DE.

五.相似三角形的性质
1、相似三角形的对应角相等,对应边成比例
2、相似三角形对应高的比、对应中线的比与对应角平分线的比都等于相似比
3、相似三角形周长的比等于相似比
相似三角形对应高的比,对应中线的比与对应角平分线的比都等于相似比.一般地,我们有:相似三角形对应线段的比等于相似比.具体如下表:

例11.求证:相似三角形对应边上的中线之比等于相似比.
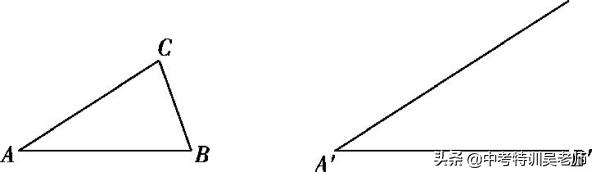
要求:如图,(1)根据给出的△ABC及线段A'B',∠A'(∠A'=∠A),以线段A'B'为一边,在给出的图形上用尺规作出△A'B'C',使得△A'B'C'∽△ABC,不写作法,保留作图痕迹;(2)在已有的图形上画出一组对应中线,并据此写出已知、求证和证明过程.
4、相似三角形面积的比等于相似比的平方。
证明:已知△ABC∽△A'B'C',相似比为k,AD、A'D'分别为△ABC,△A'B'C'的高,
则有S△ABC=1/2BC·AD,S△A'B'C'=1/2B'C'·A'D',
所以


易错点:易混淆相似三角形的面积比与等底或等高三角形的面积比.
解题过程中,要分清相似三角形的面积比等于相似比的平方,而等底或等高的三角形的面积比等于对应底或高的比.

例12.如图,在△ABC中,M,N分别为AC,BC的中点.若S△CMN=1,则S四边形ABNM= .

六.相似三角形相似模型
1、平行模型

2、反平行模型

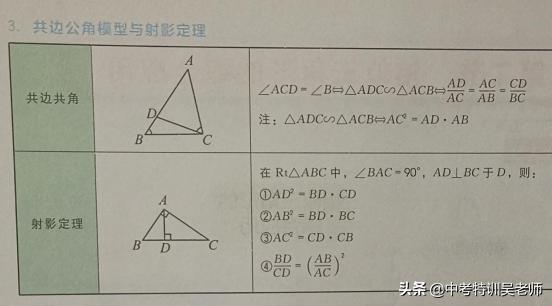
3、共边公角模型与射影定理
4、一线三角模型与三垂直模型


七.相似多边形
1、如果两个边数相同的多边形的对应角相等,对应边成比例,那么这两个多边形叫做相似多边形。相似多边形对应边的比叫做相似比(或相似系数)
2、相似多边形的性质
①相似多边形的对应角相等,对应边成比例
②相似多边形周长的比、对应对角线的比都等于相似比
③相似多边形中的对应三角形相似,相似比等于相似多边形的相似比
④相似多边形面积的比等于相似比的平方
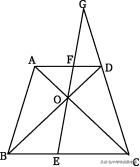
例13.如果四边形ABCD的对角线交于O,过O作直线OG∥AB交BC于E,交AD于F,交CD的延长线于G,求证:OG2=GE·GF.
例14.如图,矩形DEFG的边EF在△ABC的边BC上,顶点D、G分别在边AB、AC上.已知AC=6,AB=8,BC=10,设EF=x,矩形DEFG的面积为y,则y关于x的函数关系式为 .