文章目录
- 从线性回归说起
- sigmond函数
- 推广至多元场景
- 似然函数
- 最大似然估计
- 损失函数
- 梯度下降法求解
- 结尾
【提示:头条号编辑器不支持Markdown,因此涉及公式的部分全部转为图片显示】
今天梳理一下逻辑回归,这个算法由于简单、实用、高效,在业界应用十分广泛。注意咯,这里的“逻辑”是音译“逻辑斯蒂(logistic)”的缩写,并不是说这个算法具有怎样的逻辑性。
前面说过,机器学习算法中的监督式学习可以分为2大类:
- 分类模型:目标变量是分类变量(离散值);
- 回归模型:目标变量是连续性数值变量。
逻辑回归通常用于解决分类问题,例如,业界经常用它来预测:客户是否会购买某个商品,借款人是否会违约等等。
实际上,“分类”是应用逻辑回归的目的和结果,但中间过程依旧是“回归”。
为什么这么说?
因为通过逻辑回归模型,我们得到的计算结果是0-1之间的连续数字,可以把它称为“可能性”(概率)。对于上述问题,就是:客户购买某个商品的可能性,借款人违约的可能性。
然后,给这个可能性加一个阈值,就成了分类。例如,算出贷款违约的可能性>0.5,将借款人预判为坏客户。
1.从线性回归说起
考虑最简单的情况,即只有一个自变量的情况。比方说广告投入金额x和销售量y的关系,散点图如下,这种情况适用一元线性回归。

线性回归的介绍文章戳这里:用人话讲明白线性回归LinearRegression
但在许多实际问题中,因变量y是分类型,只取0、1两个值,和x的关系不是上面那样。假设我们有这样一组数据:给不同的用户投放不同金额的广告,记录他们购买广告商品的行为,1代表购买,0代表未购买。
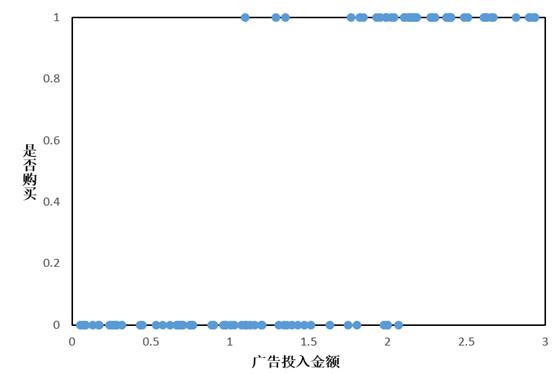
假如此时依旧考虑线性回归模型,得到如下拟合曲线:


这种形式,非常像单位阶跃函数:

图像如下:

我们发现,把阶跃函数向右平移一下,就可以比较好地拟合上面的散点图呀!但是阶跃函数有个问题,它不是连续函数。
理想的情况,是像线性回归的函数一样,X和Y之间的关系,是用一个单调可导的函数来描述的。
2.sigmond函数
实际上,逻辑回归算法的拟合函数,叫做sigmond函数:

函数图像如下(百度图片搜到的图):

sigmoid函数是一个s形曲线,就像是阶跃函数的温和版,阶跃函数在0和1之间是突然的起跳,而sigmoid有个平滑的过渡。
从图形上看,sigmoid曲线就像是被掰弯捋平后的线性回归直线,将取值范围(−∞, ∞)映射到(0,1) 之间,更适宜表示预测的概率,即事件发生的“可能性” 。
3.推广至多元场景
在用人话讲明白梯度下降Gradient Descent一文中,我们讲了多元线性回归方程的一般形式为:

到目前为止,逻辑函数的构造算是完成了。找到了合适的函数,下面就是求函数中的未知参数向量β了。求解之前,我们需要先理解一个概念——似然性。
4.似然函数
我们常常用概率(Probability) 来描述一个事件发生的可能性。
而似然性(Likelihood) 正好反过来,意思是一个事件实际已经发生了,反推在什么参数条件下,这个事件发生的概率最大。
用数学公式来表达上述意思,就是:

因此,最优β,就是使当前观察到的数据出现的可能性最大的β。
5.最大似然估计
在二分类问题中,y只取0或1,可以组合起来表示y的概率:



因为一系列的xi和yi都是我们实际观测到的数据,式子中未知的只有β。因此,现在问题就变成了求β在取什么值的时候,L(β)能达到最大值。
L(β)是所有观测到的y发生概率的乘积,这种情况求最大值比较麻烦,一般我们会先取对数,将乘积转化成加法。
取对数后,转化成下式:

接下来想办法求上式的最大值就可以了,求解前,我们要提一下逻辑回归的损失函数。
6.损失函数
在机器学习领域,总是避免不了谈论损失函数这一概念。损失函数是用于衡量预测值与实际值的偏离程度,即模型预测的错误程度。也就是说,这个值越小,认为模型效果越好,举个极端例子,如果预测完全精确,则损失函数值为0。
在线性回归一文中,我们用到的损失函数是残差平方和SSE:

很遗憾,这个不是凸函数,不易优化,容易陷入局部最小值,所以逻辑函数用的是别的形式的函数作为损失函数,叫对数损失函数(log loss function)。
这个对数损失,就是上一小节的似然函数取对数后,再取相反数哟:

这个对数损失函数好理解吗?我还是举个具体例子吧。
用文章开头那个例子,假设我们有一组样本,建立了一个逻辑回归模型P(y=1)=f(x),其中一个样本A是这样的:
公司花了x=1000元做广告定向投放,某个用户看到广告后购买了,此时实际的y=1,f(x=1000)算出来是0.6,这里有-0.4的偏差,是吗?在逻辑回归中不是用差值计算偏差哦,用的是对数损失,所以它的偏差定义为log0.6(其实也很好理解为什么取对数,因为我们算的是P(y=1),如果算出来的预测值正好等于1,那么log1=0,偏差为0)。
样本B:x=500,y=0,f(x=500)=0.3,偏差为log(1-0.3)=log0.7。
根据log函数的特性,自变量取值在[0,1]间,log出来是负值,而损失一般用正值表示,所以要取个相反数。因此计算A和B的总损失,就是:-log0.6-log0.7。
之前我们在用人话讲明白梯度下降中解释过梯度下降算法,下面我们就用梯度下降法求损失函数的最小值(也可以用梯度上升算法求似然函数的最大值,这两是等价的)。
7.梯度下降法求解
要开始头疼的公式推导部分了,不要害怕哦,我们还是从最简单的地方开始,非常容易看懂。



加上求和号:

8.结尾
文章写到这里就结束了,其实逻辑回归还有很多值得深入学习和讨论的,但是“讲人话”系列的定位就是个入门,我自己目前的水平也有限,所以本篇不再往后写了。
最后,欢迎各位一起学习讨论~
,




