这两天,广东省数学中考题(广州,深圳不采用本套试卷)的难度系数备受关注,从去年的超级难到今年的特别简单,过山车似的难度系数让学霸缓不过神来。
试卷难不难,先看压轴题。说实话,广东省2022年中考数学压轴题,说它是史上最简单可能有点夸张,但这道题的确不难。

广东中考数学压轴题。
所有人都知道这道题很简单,网上也有很多人都在做这道压轴题。那么这道很简单的压轴题是不是毫无亮点呢?从数学学习的角度而言,排除中考的因素,这还真的是一道非常不错的二次函数题目,它有很多种解法,每一种解法都独具特点,尤其对初步接触二次函数的学生来说,这道题真的很值得探讨。
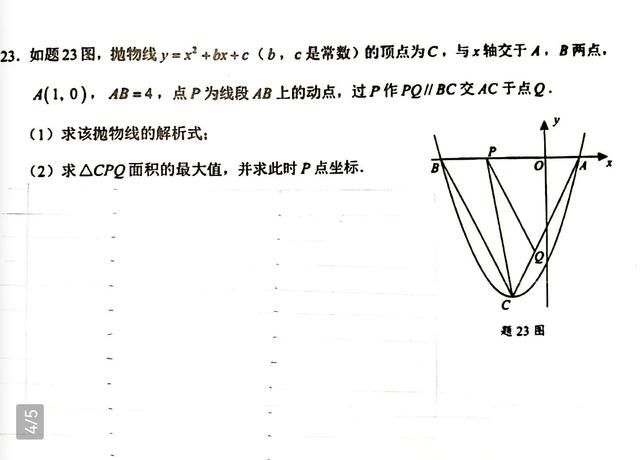
广东中考数学压轴题。
今天我也来分享一下我的解题方法,这道题真的有很多解题方法,每种方法的思路是不同的,我先分享一种我认为最快捷的解题方法,不服的可以来挑战。[灵光一闪]
方法1:不用证明相似,也不用求直表达式,用平行线分线段成比例定理即可搞定。具体步骤如下图。

最简单的方法。
三角形PCQ和三角形PCA的面积之比,等于底边CQ与CA之比(高相等,面积之比等于底边之比),由平行线分线段成比例定理,C Q:CA=BP :BA=(m+3):4,从而得到三角形PCQ与三角形PCA之间的等量关系,得到三角形PCQ的函数关系式,再来求出最值。两三分钟可以搞掂这一问,真的很快很简单。
方法二,利用相似三角形的求解,这种方法思路比较清晰,也很简单,应当是大部分考生采用的方法。

方法二,用相似三角形求解。
但是选择哪一组相似三角形非常重要,否则会增加试题的难度。显然,选择三角形APQ相似于三角形ABC最快捷。利用相似三角形的面积比等于相似比的平方,可以表达出三角形APQ的面积。三角形APC的面积减去三角形APQ的面积,就表示出三角形PCQ的面积,再来求最值。
方法三,求直线的表达式和Q点的坐标。这也是非常常规的一种方法,但对于本道题来说,略显得有点复杂。不过这种方法是非常重要和常规的。

解题方法三。
求出BC和直线AC的表达式。因为BC和PQ平行,把直线PQ的表达式表示出来。联立直线PQ和AC的表达式,求出Q点的坐标,再把三角形PCQ的面积表达式求出来。

寻找每道数学题的闪光点
所以说这一道压轴题的确实够简单,但你如果愿意深入探究,也能发现他的一些闪光点。其实这道题还有其他很多种方法,包括也可以用水平宽乘铅垂高表示三角形的面积,或者用相似三角形求三角形的高等等。
以上内容供你参考。
,