论文中如何分析pca（看完这篇图解PCA面试再也不担心）

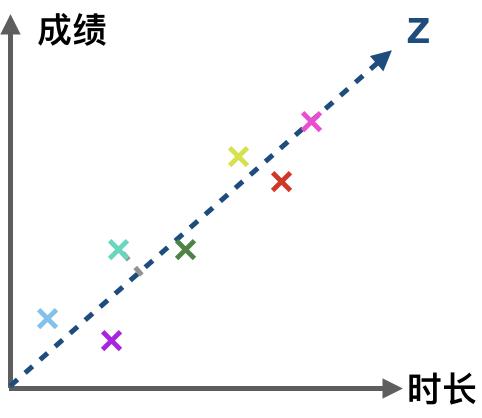
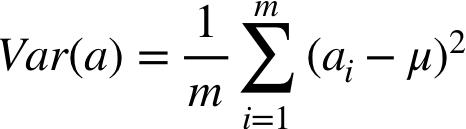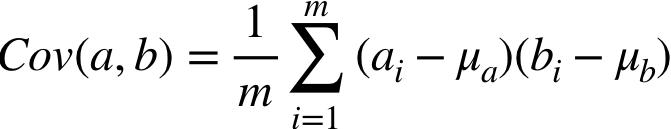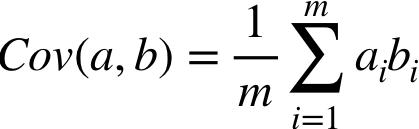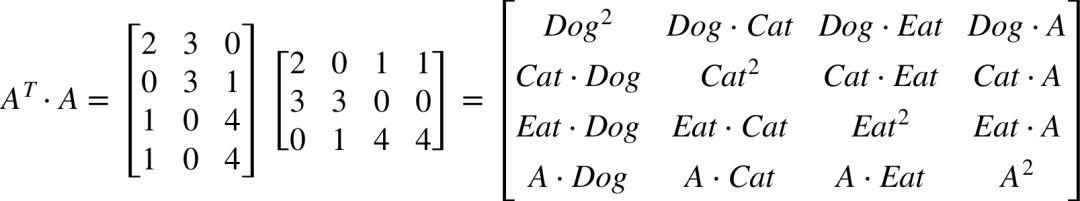作为经典降维方法，PCA（Principal components analysis）是机器/算法学习工程师及数据分析师面试时 99% 可能会问到的问题。由于缺乏对 PCA 的物理和几何意义的深入理解，此题也成为一道颇有难度的问题。本文旨在通过形象化的表达和数学推导带你深入理解PCA。为什么要 PCA

PCA 是为了降低特征的维度。在实际工作中，可能会遇到特征维数过多，且部分特征具有一定相关性。如：在一个学生成绩数据集中，一个特征是学习时长，另一个特征是成绩，一般来讲，学习时间越长，越容易取得好成绩，即时长与成绩呈正相关。因此没必要用两个维度（时长和成绩）表达这一特征。我们可以找出另一个维度，表现这两个特征，且不会带来过多信息损失。

由图可知，可以用数据点在 Z 轴上的投影表达时长与成绩两个维度的数据。一个平面上的数据就被映射到了一条线当中，即二维特征向一维特征的转换。

如何 PCA

为了让高维度特征向低维度特征的映射更加精确，在上例中，我们需要找出一条使得所有的实例（entity）到坐标轴垂直距离（图中虚线部分）最短的一条坐标轴 Z。同时这条坐标轴也满足数据在其上散布最广。

在数学中，我们用方差定义数据的离散程度，公式如下：

其中 m 表示 entity 的总数，即 m 个实例，a(i) 是第 i 个实例的属性 a， μ 表示该属性在所有实例当中的均值（mean）。再来看看我们一会儿要用到的另一个公式：协方差公式，表示两个向量之间的相关性：

有些教材中会把 m 写成 m-1，请忽略，实际没有本质区别。

在上面两个公式中，均值被反复用到，由于进行矩阵运算时，减去均值的操作不方便，我们可以提前让所有的特征减去其均值，即 a(i) := a(i) - μ(a)。这个操作叫做 mean normalization。因此方差公式和协方差公式就可以被简化成：

这在将来做矩阵运算时很有帮助。

回到问题，我们想找出指定的 K 个维度，使数据在这 K 个维度上损失最少 -> 散布最广 。除了用方差衡量我们要取的坐标轴外，还应考虑数据在新维度上的散布不具有任何相关性，回到最开头的问题，在原始数据中，两个属性（学习时长和成绩）具有相关性，我们希望降维来去除这种相关性，这也是 PCA 的意义之一。

回顾上面的公式，协方差表示了向量间的相关性，协方差为 0，向量完全不相关，向量互相正交。

问题被转化成了，我们希望找出一组基向量（需要是标准正交基），数据在这组基向量构成的空间中表示时，任何两个属性间相关性为零。我们取出数据散布最广的前 K 个维度，就是我们希望求取的新坐标系（基向量），将原本的数据以新的基向量为参考系表示出来，就是数据压缩后的结果。

假设 A 是原始数据集，每一行代表一个文档，每一列代表指定单词在文档中出现的次数。

计算一下 A 的转置与 A 相乘。

把矩阵的每一项除以 entity 的个数 m，你会发现，这是一个实对称矩阵，对角线上的值是其方差（红圈部分），其他值对应两个属性之间的协方差（以黄色下划线部分为例）。我们希望找出一个新的基向量所代表的空间 P（每列是一个基向量），原始的数据 A 在 P 的衡量下的新的表示方式为 Z，即 Z = AP，如果 (1/m)*Z(T)Z 能变成一个对角矩阵（除对角线外其余元素为 0），那么 P 就是我们想找的那组基向量。

在数学中一个实对称矩阵有 3 个性质：

1. 不同特征值对应的特征向量必然正交
2. k 重特征值必定对应 k 个线性无关的特征向量

左侧公式展开了 Z 的协方差矩阵，右侧公式是矩阵的特征值/奇异值分解。可以发现特征值分解后，特征向量所组成的矩阵正好是一个对角矩阵，因此特征值分解原数据矩阵 A 后，特征向量所组成的矩阵即为要求的矩阵 P。

我们已经求出了新的空间 P，那么如何选取 P 最重要的 N 个维度，去除其他维度，以进行降维呢？

根据上面的推导，我们认为 Σ 和 Z 的协方差矩阵 (1/m)*Z(T)Z 相等，就是说，Σ 上对角线的值就是 Z 的每个属性的方差，由此我们可以确定，如果将 Σ 对角线上的元素按降序排列，取出 U 的前 K 个值，那么降维就完成了。

,