利用初等变换求解数列极限,主要包括裂项,分组,求和等。在高中时我们开始接触数列,学习了等比数列,等差数列,以及等差和等比的乘积数列,对于求已知数列的通项公式,以及求数列的前n项和,我们有各种方法,比如说裂项法,分组法,倒序相加法,错位相减法等等,今天我们将利用高中时代所学过的方法去解决考研数学中关于数列求极限的问题,主要思想是通过已知方法将复杂数列简单化进而求解其极限。通过以下几个例题呈现。
例题1.用的方法是分子有理化的方法:

例题2. 利用等比数列前n项和公式求极限,对于这类极限我们可以进一步总结一个通用公式,大家可以先自己试着写写,下节课揭晓答案。

例题3.利用裂项法求极限:

例题4.利用分组法求极限:

作业1.利用错位相减法求下列极限:
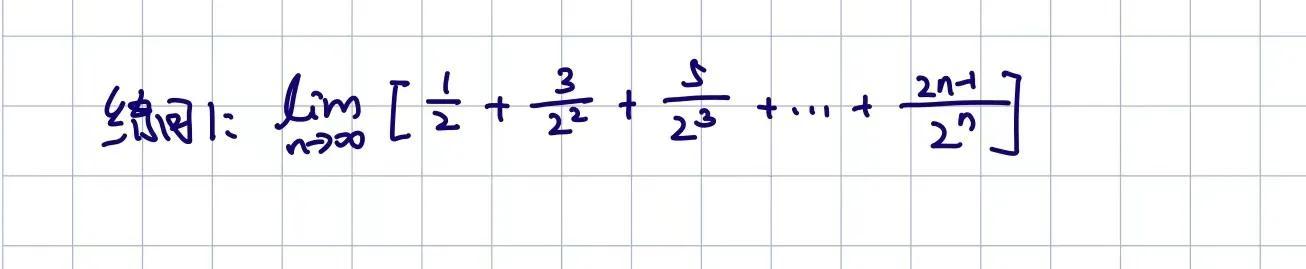
作业2.利用适当方法求下列极限:

大家务必要反复练习,并且将每种方法融会贯通,做到举一反三!我们下次课再会!
,




