
你知道地球是什么形状吗?

亚里士多德说:地球是圆形的。
物理老师说:地球是椭圆形的。
网友说:地球是梨形的。
我说:我信你个鬼,你个糟老头子……
地球是梨形的,这实在是一件让人啼笑皆非的事情。
自从古希腊哲学家毕达哥拉斯(Pythagoras)提出大地是球形的观点之后,“地球是个球”的理论就开始被不断普及,并逐渐为世人所接受,时至今日已在世间流传了数千年之久。
事到如今,无论从天文学书籍的插图,还是太空拍摄的照片来看,地球的形状都几乎是一个标准的球体,就算在绝大多数人的固有观念里,地球最起码也应该是椭圆形的。
然而近几年来,这个本该如钛合金一样坚固的真理,却莫名其妙地遭到了不少人的质疑和反对。因为很多“科普文章”忽然摆出了一张极具权威性的3D彩色模型,煞有介事地告诉大家:这才是地球的真实面目,它并不像你们想象中那么圆。

哎哟我的妈呀,真是辛苦科普上千年,一夜回到解放前。而且这个歪瓜裂枣的玩意儿也实在忒丑了点,四处宣扬咱们的地球妈妈长成这样,就不怕把她老人家气得发抖,直接整出个全球十级大地震么?
不过,假如你机智如我的话,见到这张图可能会立刻产生一个疑问:如果地球的形状是酱紫的,那为啥从太空拍摄的地球,看上去像乒乓球一样圆呢?
可是你如果真的这样问了,那些笃信地球就这么丑人往往会一本正经地告诉你:那是因为有水啊,把海水全部抽空,地球就是酱紫的了。
呃……听上去真的好有道理,要不是小时候读过几年书,我差点就信了。

但不管信不信,咱们必须承认上面那张图并不是别有用心的人故意画出来丑化地球的。而是通过严谨的计算后模拟出来的,并且出自于权威机构——国际地球重力场模型中心(ICGEM)。尽管如此,把它解释成抽干了水的地球,却是教科书式的张冠李戴。
那么问题来了:这奇形怪状的玩意儿,究竟是个什么玩意儿,整出来干啥玩意儿?
这就要从地球的重力异常现象谈起了。
什么叫重力异常?水一般都是从高处向下流的,但如果某个地方情况反过来了,水往高处流,这就叫重力异常。
就像酱紫——

余晖效应造成的视错觉现象
不过,稍微有一点物理常识的人都知道,这种情况在现实中是不可能存在的,所以咱们要说的是另一种真实存在的重力异常。
众所周知,地球并不是一个平滑的球体,它的表面山峦叠嶂、沟壑纵横,俗称“麻麻赖赖的,一点儿都不圆润”。
不圆润咋办呢?很简单,搞文玩的都知道:盘它!
相信我,真的是“盘它”,我没开玩笑。
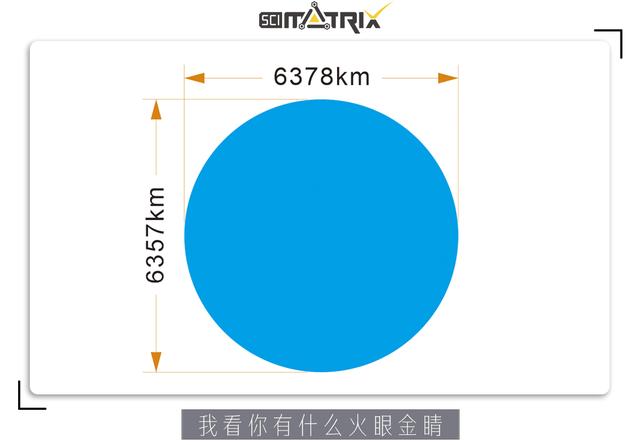
你或许听说过,地球的赤道半径和极半径分别是6378公里和6357公里。然而你一定没想到,在目前全球统一使用的世界大地测量系统(WGS 84)中,地球的标准赤道半径实际上为637813700厘米,标准极半径为635675231.42厘米。
“.42厘米”意味着地球半径已经被精确到了毫米,要达到这个精度,把地球“盘圆”无疑是首要前提,否则随便来一场八级大狂风,刮走二两土,地质学家们全都哭死在厕所里了不是?
当然,咱们不可能真的把地球抓在手里搓圆润,但咱们可以在建立几何模型时,用科学的方法把它“画圆润”啊。
具体是怎么画的咱们就不赘述了,大致就是经过一系列猛如虎的测量和计算之后,定义一个理想的平均海平面(MSL),再以它为基准来建立一个光滑的地球模型。
这个模型在大地测量学中被称为“参考椭球”,你可以把它理解为一个理想化的地球模型,我们平常所指的地球半径,实际上就是参考椭球的半径;地球的经纬点也是建立在参考椭球上的。

那么,这个被盘圆了的地球,跟重力异常有什么关系呢?
坦白讲,不仅有关系,甚至可以说参考椭球就是导致重力异常的“罪魁祸首”。
由于参考椭球是理想化的地球,没有密度这个重要的物理性质,或者说它的密度被视为均匀的,因此以它的各项参数结合万有引力计算而来的地球重力,只会受到纬度的影响,在经度上是以完全相同的值均匀过渡的,这被称为正常重力(normal gravity)。
但实际上,地球内部构造以及地底矿产的不规则分布,决定了地球的密度是不均匀的,重力分布也是毫无规则的。这就导致以参考椭球为依据计算出来的正常重力,与各经纬点所对应的实际地点测量出来的重力之间存在差异——这种因地质密度导致的重力和正常重力不吻合的现象,就被称为“重力异常(gravity anomaly)”。
通过重力异常情况来分析及描述全球重力场的精细结构,是十分重要的工作,对于大地测量及航天领域而言尤为如此。否则发射火箭时,因为重力没算清楚,落到你家屋顶上了,你上哪说理去?
不过在某些工作中,咱们也需要对重力异常进行改正。改正的方式有很多种,如高度改正、地形改正、均衡改正等等。
至于具体是怎么做的,咱们也不赘述了,反正就是又经过一系列猛如虎的测量和计算之后,找到了一个表面“波澜起伏”,但重力位完全相等,且最能与平均海平面相重合的不规则曲面,再把地面的实测重力值归于这个面上,这个面叫做“大地水准面(Geoid)”。
通俗来说:重力异常改正就是把好不容易盘圆的地球,又给整毛糙了。把大地水准面绘制在平面图上,就是下面酱紫的。

这两张图中,红色不规则圆环是大地水准面,黑色圆环是参考椭球。值得注意的是,图上标注的30m、40m、70m、-100m等参数,指的是大地水准面在该位置实际偏离了参考椭球多少米。
也就是说,大地水准面与参考椭球的最大实际偏差只有100多米,这对于参考椭球的半径而言根本可以忽略不计(别忘了参考椭球的半径就是地球的半径)。所以为了让人能明显看出大地水准面和参考椭球的差异,它的起伏是而被刻意放大了的。
放大了多少呢?
答案是:按比例放大了10000倍。
是的,你没数错0,是整整放大了一万倍。若非如此,在这个尺度下大地水准面和参考椭球就是两个完全重合的正圆形,根本看不出任何差异。
有意思的是,起伏被放大一万倍之后,从赤道方向观看,大地水准面的形状就像个大鸭梨,于是便有人就拿着这张“大鸭梨的图片”,无比激动地四处宣称地球是梨形的了。
哎,这些人啊,根本没搞懂图上究竟画了个啥,就开始浮想联翩了。
说到这里,你应该知道文章开头那个歪瓜裂枣的地球模型是个啥玩意儿了。
没错,它就是大地水准面的3D模型,并且同样是表面起伏被放大了一万倍的3D模型,如果严格按照数据来建立,它实际上也是一个非常光滑的大圆球。

所以,以后再也不要说地球是梨形的,或者说它像个歪瓜裂枣的土豆了,它甚至都不应该被称为椭圆形。尽管从数据来看,地球的极半径小于赤道半径,然而它们的实际差异仅仅只有大约21.3km。
如果你想象不出对于半径6378km—6357km的地球而言,21.3km的差异意味着什么,那你就想象一下,倘若一个地球仪在横向和纵向上的半径分别是6.378厘米和6.357厘米,你能通过区区0.2毫米的差异看出它是椭圆形吗?
如果你能看出来,我敬你上辈子是个孙悟空。
换言之,地球是椭圆形的说法仅仅只能体现在数据中。可如果非要拿数据来说话,则现实中没有任何圆球不是椭圆形的。事实上你随便抓一个乒乓球、篮球、足球或任意阿猫阿狗球,它的半径误差都比地球大得多。
除此之外,地球表面的最高点珠穆朗玛峰海拔约8844.86米,最低点马里亚纳海沟的深度约11034米,最大落差也只有大约20公里。当地球被缩小到半径6厘米的尺度时,珠穆朗玛峰的高度只有0.08毫米,而马里亚纳海沟也不过是一个0.1毫米深的划痕,这意味着你需要用高倍放大镜才能勉强看见珠穆朗玛峰和马里亚纳海沟。
同时这也就意味着,地球哪怕被抽干了海水,也比你这辈子见过的绝大部分圆球都更圆、更光滑。
所以如果以后再有人问你地球是啥形状,千万别说椭圆形了。
你应该直接告诉他:地球是个球!






