利用统计学正态分布确定存货周转率
上一篇文章提出了应用经济批量结合最低库存量计算目标周转率(KPI)的方法,虽然该方法从科学角度是最准确的,成本与采购最优的方案,但受限于受到的参数影响多,变量取值不方便,目前在国内中小企业中少有人使用该方法来进行库存控制,接下来笔记使用统计学中的正态分布法来确定最大库额以达到计算目标存货周转率的方法。

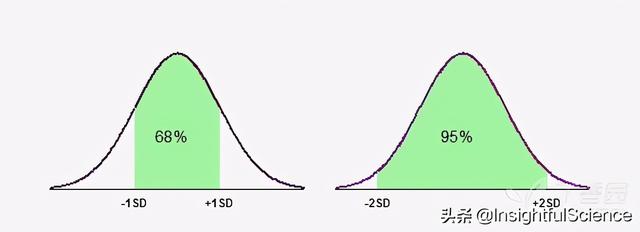
正态分布是一个在数学、物理及工程等领域都非常重要的概率分布,在统计学的许多方面有着重大的影响力,正态曲线呈钟型,两头低,中间高,左右对称因其曲线呈钟形,因此人们又经常称之为钟形曲线。正态分布图见下图:
正态分布有以下特征:
1、数据在(平均数-标准差)至(平均数 标准差)的区间内的概率为68.3%;
2、数据在(平均数-标准差*2)至(平均数 标准差*2)的区间内的概率为95.4%;
3、数据在(平均数-标准差*3)至(平均数 标准差*3)的区间内的概率为99.7%;
依据这一特性,我们是不是可以将库存设定在2个标准差加上平均数的水平就能控制95.4%以上的水平了,当然,如果认为这样还不够就取3个标准差。
这里我们需要计算两个数据就能设定最高库存量了,一是标准差、二是平均数。
一、标准差如何计算

标准差又常称均方差,是离均差平方的算术平均数的平方根,用σ表示。在概率统计中最常使用作为统计分布程度上的测量。标准差是方差的算术平方根。公式如下:
读者是不是感觉太复杂,还好标准差公式已在电子表格软件中有相应的函数能直接使用,不需要大家去具体按这个公式来计算,电子表格求标准差的函数(STDEV.P),具体如何计算我们通过下面的案例进行展示。
二、平均数如何计算
首先,这里的平均数是一个区间发出物料(存货)的平均数,如果按上文案例来说明,A公司以单价10元每年购入某种材料8000件。每次订货费用为30元,资金年利息率为12%,单位维持库存费按所库存货物价值的18%计算。每次订货的提前期为2周。
按该案例每年购入材料8000件,每月具体使用数据如下图:

1、月平均值为666.67件;
2、应用STDEV.P函数计算出的标准差为40.28;
3、最高库存=666.67 2*40.28=747.23件;
4、存货周转率设定目标=8000/374=21次,周转天数17天。
按此模型计算出来的最高库存为747.23件,按上篇文章计算出来的为711件,如果从经济合理性来看,肯定是第一个方案更优,但计算复杂,受其他因素影响大,现在读者可以考虑接下来用这个方法来控制库存水平了,当然可能还有一些朋友发现我这个模型中每月的用量较为均衡,如果出现大的用量波动是否仍然有效,那我们假设每月用量如下图:

1、月平均值为666.67件;
2、应用STDEV.P函数计算出的标准差为336.9
3、最高库存=666.67 2*336.9=1340件
4、存货周转率设定目标=8000/670=12次,周转天数30天。
模型中最大用量值为1200件,我们设定的最高库存1340件,应该是覆盖到了这个风险因素。
总结:本模型的优点计算与取值都相对简单,虽然本模型不用计算最低库存量了,但我们仍要关注因低于最低库存量导致的缺货损失,同时需要关注预测业务量的准确性,该模型同时适用于对应收账款,货币资金账户余额的风险控制。
,