数据的统计分析（统计数据的分析）

一. 基本概念

1.平均数：一般地，对于n个数x1，x2,..xn,我们把叫做这n个数的算术平均数，简称平均数

2.加权平均数：

3.中位数：将一组数据按从小到大的顺序（或由大到小）的顺序排列，如果数据的个数是奇数，则处在中间位置的数为这组数据的中位数，如果数据的个数为偶数，则中间这两个数的平均数为这组数据的中位数。

4.众数：我们将一组数据中出现次数最多的那个数据叫做这组数据的众数

5.方差：各数据与他们的平均数的差的平方的平均数

方差是刻画数据的波动程度的

方差越大，数据波动越大，越不稳定

方差越小，数据波动越小，越稳定

6.用样本估算总体：用样本估算总体是统计的基本思想，如果考察的总体包含很多个体，或者考察本身带有破坏性，考察总体平均数和总体方差时，实际常常用样本平均数，样本方差来估算总体平均数，总体方差

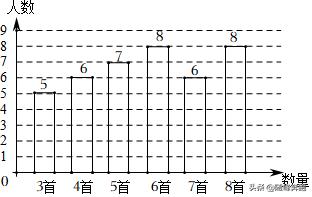
例：为积极响应“弘扬传统文化”的号召，曲江一中组织初一年级1200名学生进行经典诗词诵读活动，并在活动之后举办经典诗词大赛，为了解本次系列活动的效果，学校团委在活动启动之初，随机抽取40名学生调查“一周诗词诵背数量”，根据调查结果绘制成的统计图如图所示．

大赛结束后一个月，再次抽查这部分学生“一固诗词诵背数量”，绘制成统计表如表：

请根据调查的信息分析：

（1）活动启动之初学生“一周诗词诵背数量”的众数为 　 　，中位数为 　 　；

（2）求在大赛结束后一个月，抽查的这部分学生一周诗词背诵数量的平均数；

（3）估计大赛后一个月初一学生一周诗词诵背6首及6首以上的人数．