【欧拉定理及向量证明】
三角形三条边的中垂线交于一点叫作外心,三条中线交于一点叫作重心,三条高所在直线交于一点叫作垂心.瑞士数学家欧拉(1704-1783)发现任意三角形的外心、重心、垂心总在一条直线上,因此这条直线被称为欧拉线.
这个结论用几何方法证明比较繁琐,利用向量方法可以作出简单的证明.


【例题精析】

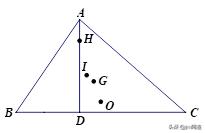



【强化练习】
一、单选题
1. 著名数学家欧拉提出了如下定理:三角形的外心、重心、垂心依次位于同一直线上,且重心到外心的距离是重心到垂心距离的一半.此直线被称为三角形的欧拉线,该定理则被称为欧拉线定理.设点O,H 分别是直角三角形ABC 的外心、垂心,点H和点B 重合,且M为BC中点,则( )


二、多选题
2. 瑞士数学家欧拉在1765年发表的《三角形的几何学》一书中有这样一个定理:“三角形的外心垂心和重心都在同一直线上,而且外心和重心的距离是垂心和重心距离之半”这就是著名的欧拉线定理 .设三角形ABC 中,点O、H 、G 分别是外心、垂心、重心,下列四个选项中结论正确的是 ( )



3. 著名数学家欧拉提出了如下定理:三角形的外心、重心、垂心依次位于同一直线上,且重心到外心的距离是重心到垂心距离的一半.此直线被称为三角形的欧拉线,该定理被称为欧拉线定理.已知三角形ABC的外心为O,垂心为H,重心为G,且AB=2,AC=3,则下列说法正确的是 ( )


4. 著名数学家欧拉提出了如下定理:三角形的外心、重心、垂心依次位于同一直线上,且重心到外心的距离是重心到垂心距离的一半,此直线被称为三角形的欧拉线,该定理被称为欧拉线定理.已知三角形ABC的外心为O,重心为G,垂心为H,点M为BC中点,且AB=4,AC=2,则下列各式正确的有 ( )