在“今日头条”上读到“公元前240年,他把棍子插在地上,结果成功测出了地球周长”一文,说的是埃拉托斯特尼(Erathosthenes,约公元前276-约公元前195/194)最早测出地球周长的“壮举”:大约在公元前240年夏至那天,他在亚历山大港的地上插了根棍子,在正午时根据棍子投出的影子测出太阳距离天顶的角度大约为7°(应该是7.2°);由于他知道这天正午他家乡赛印城(Cyene,也就是今天的阿斯旺Aswan)直立的棍子没有日影(因为那里处在北回归线上),又知道赛印城到亚历山大城的距离是800希腊里,所以用简单的比例方法就可以求出地球的周长(图1):
7.2°/亚-赛间的距离 = 360°/地球周长
地球周长=(360° X 亚-赛间的距离)/7.2°
= 50 X 800希腊里 = 40000希腊里

图1:埃氏测量地球周长的几何原理 图1:埃氏测量地球周长的几何原理
至于埃氏是如何测出7.2°这个角度的,那也很简单(图2):只要测出棍子的高度h,影长l,那就不难知道太阳光与棍子的夹角α——也就是此刻太阳的天顶角。

图2 α角的测量原理
但是我要提醒大家的是,这看似简单的方法其实并不简单:这倒不是说那根棍子不是随便插的,而要保持直立——因为这用个铅锤就可以解决;也不是说亚-赛两地之间的距离不容易测量——因为当时埃及有职业的测距师;更不是说只有当亚历山大港(东经29°55′)和赛印城(东经32°54′)处在同一条南北线上(地理经度相同)时,上述这个计算才能奏效——其实今天知道二者之间的地理经度的差别不到区区3°,完全可以忽略不计;而是说,这里面要用到今天被称作三角函数的东西——那个用专门用来进行三角形边-角互算的数学工具——比如这里的已知两边求一角。但是,别忘了,在埃氏生活的年代,世界上还没有这东西。发明三角学的人——天文学家伊巴谷(Hipparchus of Nicaea,约公元前190-约公元前120)——那时还没有出生。
传说,埃氏当初是在一本名叫《论地球之测量》的著作中描写上述测量方法的,但这本书其实早已失传。现在关于这件事情的最早记载来自希腊天文学家克莱奥美德斯(Cleomedes)的《论天体之圆周运动》一书。我们并不清楚克氏生活在哪个年代。由于他在书中引用过伊巴谷而没有引用过托勒密(Ptolemy,约公元100-公元170),可以知道他应该生活在伊巴谷之后和托勒密之前。但是,如果他说埃氏是通过测量那根棍子和它在夏至日正午影子的长度测出那个7.2°角的,那就应该是他的推测,原因是:埃氏时代还没有三角学和三角函数这些东西;而到了克氏时代,伊巴谷早已经发明的三角学方法——也就是今天被称为弦函数(等效于正弦函数)——所以克氏就有可能设想埃氏是用这种方法测出那个角度的。果真如此,那其实也只是克氏对历史的一种“反历史的”(Anachronistic)解读——埃氏时代的的确确还没有出现这样的数学工具,因为正是由于没有这样的工具,差不多与埃氏同时代的希腊天文学家阿利斯塔克(Aristarchus,约公元前310-约公元前230)在《论日月的距离与大小》一文中讨论日月和地球三者的大小和距离时,就只能给出相对的比例区间,而不是一个一个的具体数值。
当然,虽然还没有三角学,但埃氏还是可以测出那个角度的,因为他完全可以用一种更加简单的方法——球面日晷,因为从球面日晷上可以直接读出任意时刻太阳的天顶角,当然也包括夏至日正午的太阳天顶角α——这比在地上插根棍子,然后通过当时还不存在的三角学计算出α要简单得多!而球面日晷在埃氏的时代早已经被发明出来了。当然,使用这一简单方法需要有一些简单的假定,例如:
第一,地球确实是一个球体,
第二,太阳离地球足够远,以至可以认为太阳光是平行照射到地面的。
后人往往会以自己时代的知识和观念来理解前人,就像克氏和现代的许多科学史家会以后来的科学知识来理解埃氏的工作一样。有的时候,后人在理解前人时,往往还会使用一些在前人时代并不存在的概念,比如我在这篇文章中使用了“三角函数”这个词。殊不知,“函数”这个数学概念是十八世纪才产生的。当伊巴谷发明出今天所谓的“弦函数”时,他自己应该有自己的叫法,但肯定不会是叫它弦“函数”吧。
其实,克氏的著作仍然留存于世。从中可以看出,克氏所描述的埃氏方法根本没有用到三角学方法,而只是”球面“日晷,对三角函数的使用确实只是现代那些理科水平太好的学者们的误读。关于克氏的记载和现代理科太好的学者的误读,可参见以下附录。
附录1:Cleomedes, On the orbits of the heavenly bodies, I, 10 (From T. L. Heath. Greek Astronomy, London (1932); via Cohen & Drabkin, A source book in Greek Science, 1948, p.149-153. ):
About the size of the earth the physicists, or natural philosophers, have held different views, but those of Posidonius and Eratosthenes are preferable to the rest. The latter shows the size of the earth by a geometrical method; the method of Posidonius is simpler. Both lay down certain hypotheses, and, by successive inferences from the hypotheses, arrive at their demonstrations.
……
The method of Eratosthenes1 depends on a geometrical argument and gives the impression of being slightly more difficult to follow. But his statement will be made clear if we premise the following. Let us suppose, in this case too, first, that Syene and Alexandria he under the same meridian circle, secondly, that the distance between the two cities is 5,000 stades;1 and thirdly, that the rays sent down from different parts of the sun on different parts of the earth are parallel; for this is the hypothesis on which geometers proceed Fourthly, let us assume that, as proved by the geometers, straight lines falling on parallel straight lines make the alternate angles equal, and fifthly, that the arcs standing on (i e., subtended by) equal angles are similar, that is, have the same proportion and the same ratio to their proper circles—this, too, being a fact proved by the geometers. Whenever, therefore, arcs of circles stand on equal angles, if any one of these is (say) one-tenth of its proper circle, all the other arcs will be tenth parts of their proper circles.
Any one who has grasped these facts will have no difficulty in understanding the method of Eratosthenes, which is this Syene and Alexandria lie, he says, under the same mendian circle. Since meridian circles are great circles in the universe, the circles of the earth which lie under them are necessarily also great circles. Thus, of whatever size this method shows the circle on the earth passing through Syene and Alexandria to be, this will be the size of the great circle of the earth. Now Eratosthenes asserts, and it is the fact, that Syene lies under the summer tropic. Whenever, therefore, the sun, being m the Crab at the summer solstice, is exactly in the middle of the heaven, the gnomons (pointers) of sundials necessarily throw no shadows, the position of the sun above them being exactly vertical; and it is said that this is true throughout a space three hundred stades in diameter.1 But in Alexandria, at the same hour, the pointers of sundials throw shadows, because Alexandria lies further to the north than Syene. The two cities lying under the same meridian great circle, if we draw an arc from the extremity of the shadow to the base of the pointer of the sundial in Alexandria, the arc will be a segment of a great circle in the (hemispherical) bowl of the sundial, since the bowl of the sundial lies under the great circle (of the meridian). If now we conceive straight lines produced from each of the pointers through the earth, they will meet at the centre of the earth. Since then the sundial at Syene is vertically under the sun, if we conceive a straight line coming from the sun to the top of the pointer of the sundial, the line reaching from the sun to the centre of the earth will be one straight line. If now we conceive another straight line drawn upwards from the extremity of the shadow of the pointer of the sundial in Alexandria, through the top of the pointer to the sun, this straight line and the aforesaid straight line will be parallel, since they are straight lines coming through from different parts of the sun to different parts of the earth. On these straight lines, therefore, which are parallel, there falls the straight line drawn from the centre of the earth to the pointer at Alexandria, so that the alternate angles which it makes arc equal. One of these angles is that formed at the centre of the earth, at the intersection of the straight lines which were drawn from the sundials to the centre of the earth; the other is at the point of intersection of the top of the pointer at Alexandria and the straight line drawn from the extremity of its shadow to the sun through the point (the top) where it meets the pointer * Now on this latter angle stands the arc carried round from the extremity of the shadow of the pointer to its base, while on the angle at the centre of the earth stands the arc reaching from Syene to Alexandria. But the arcs are similar, since they stand on equal angles. Whatever ratio, therefore, the arc in the bowl of the sundial has to its proper circle, the arc reaching from Syene to Alexandria has that ratio to its proper circle. But the arc in the bowl is found to be one-fiftieth of its proper circle.’ Therefore the distance from Syene to Alexandria must necessarily be one-fiftieth part of the great circle of the earth. And the said distance is 5,000 stades; therefore the complete great circle measures 250,000 stades. Such is Eratosthenes’ method.
附录2:一所米国大学物理系的天文学课程的网页上的一篇叫做“Astronomy 101 Specials: Eratosthenes and the Size of the Earth”的文章(注意我标红的部分):
Astronomy 101 Specials: Eratosthenes and the Size of the EarthEratosthenes' method for determining the size of the Earth was an elegant application of simple geometry to an otherwise very difficult problem. By using the difference in the elevation of the noontime sun at two different locations, he was able to measure the angular difference betwen the vertical directions at those two locations. This angular difference told him what fraction of the way around the earth separated the two locations. He then used this fraction and the measured distance between the two locations to estimate the distance around the earth (a.k.a. the circumference).
As the story goes, old Eratosthenes learned that at noon on one day a year (the summer solstice, but that's not really important), the Sun shone directly down a deep vertical well in a town called Syene, about 500 miles south of his home in Alexandria. Eratosthenes reasoned that the Sun must be directly overhead at noon in Syene at this time. He knew that the Sun was not directly overhead in Alexandria on this day, so he figured that the vertical direction in Alexandria was different from the vertical direction in Syene.
This conclusion was based on the assumption that the Sun was far enough away (compared to the distance between Syene and Alexandria) that the rays of incoming sunlight at both locations were parallel.

So how different were the vertical directions at the two locations? Well, he decided to measure this with a vertical stick in the ground called a gnomon. He watched the shadow of the gnomon on the day in question, and measured the length of the shadow at noon. The height of the stick and the length of the shadow allowed him to calculate the angle between the vertical at Alexandria (as indicated by the gnomon) and the direction of the Sun's rays at noon.
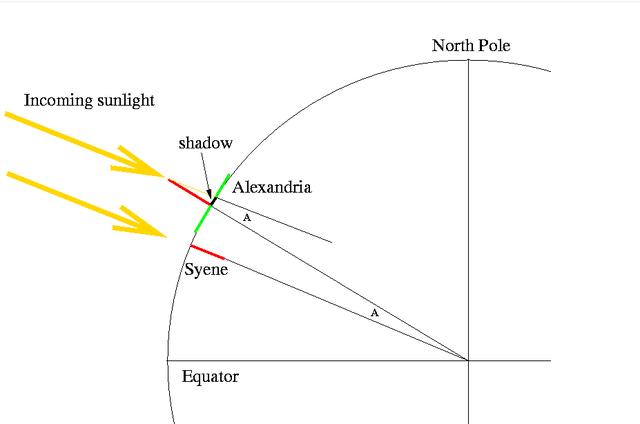
This angle, labeled “A” in the above drawing, is calculated as follows:
tan(A) = (length of shadow)/(height of gnomon)
where tan(A) is the tangent function, which was well-known at the time. By calculating this angle, Eratosthenes had calculated the angular difference between the verticals at Syene and Alexandria. Why? Because the sunward direction is the vertical direction at Syene on this day. You can see this graphically in the figure above, by noting that the sunward directions (yellow lines) are parallel, and therefore that the two angles labeled ``A'' really have the same value. (Remember? A line crossing two parallel lines makes the same angle with each line?)
So Eratosthenes made this measurement and found that the value for angle “A” is 7.2 degrees. He also knew that the actual distance between Alexandria and Syene was 5040 stades (1 stade = about 160 m) because somebody had measured it out by foot. Well 7.2 degrees is only 7.2/360ths of the way around the globe (since all the way around is 360 degrees). If that distance is 5040 stades, then the total distance around the earth must be
- total distance around the earth = 5040 stades x (360 degrees)/(7.2 degree……
(https://www.eg.bucknell.edu/physics/astronomy/astr101/specials/eratosthenes.html)
看到了吗?文中不但说“where tan(A) is the tangent function”, 而且竟然还说“which was well-known at the time.”全然不知道埃氏时代尚没有三角函数这件事,这实在让人无语。
,




