选自arXiv
作者:Guillaume Lample、Francois Charton
机器之心编译
参与:魔王
数学也可以是一种自然语言,而使用机器翻译方法就可以解决数学问题,这是 Facebook 科学家提出的用神经网络精确解符号计算的方法。

来,回顾一下常微分方程
机器学习的传统是将基于规则的推断和统计学习对立起来,很明显,神经网络站在统计学习那一边。神经网络在统计模式识别中效果显著,目前在计算机视觉、语音识别、自然语言处理等领域中的大量问题上取得了当前最优性能。但是,神经网络在符号计算方面取得的成果并不多:目前,如何结合符号推理和连续表征成为机器学习面临的挑战之一。
近日,来自 Facebook 的 Guillaume Lample 和 Franc¸ois Charton 发表了一篇论文,他们将数学(具体来说是符号计算)作为 NLP 模型的目标。更准确地讲,研究者使用序列到序列模型(seq2seq)解决符号数学的两个问题:函数积分和常微分方程(ODE)。这两个问题不管对接受过数学训练的人还是计算机软件而言都是难题。

论文链接:https://arxiv.org/pdf/1912.01412.pdf
Facebook 研究者首先提出一种可用于 seq2seq 模型的数学表达式和问题表示,并讨论了问题空间的大小和结构。然后展示了如何为积分和一阶、二阶微分方程的监督式训练生成数据集。最后,研究者对数据集应用 seq2seq 模型,发现其性能超过当前最优的计算机代数程序 Matlab 和 Mathematica。
数学也是一门自然语言
将数学表达式变成「树」
数学表达式可被表示为树的形式:运算符和函数是内部节点,运算域是子节点,常量和变量是叶节点。下面三棵树分别表示 2 3 × (5 2)、3x^2 cos(2x) − 1 和

:

Facebook 研究者将这些数学表达式看作一组数学符号组成的序列。2 3 和 3 2 是不同的表达式,√4x 和 2x 也是如此,它们都可以通过不同的树来表示。大部分数学表达式表示有意义的数学对象。x / 0、√−2 或 log(0) 也是正当的数学表达式,尽管它们未必具备数学意义。
很多数学问题都可被重新定义为对表达式或树的运算。这篇论文探讨了两个问题:符号积分和微分方程。二者都可以将一个表达式变换为另一个,如将一个方程的树映射到其解的树。研究者将其看作机器翻译的一种特例。
将树作为序列
相比于 seq2seq 模型,「树-树」模型更加复杂,训练和推断速度也更慢。出于简洁性考虑,研究者选择使用 seq2seq 模型,此类模型可以高效生成树,如在语境成分分析中,这类模型用于预测输入句子对应的句法分析树。
使用 seq2seq 模型生成树需要将树与序列对应起来。为此,研究者使用前缀表示法(又叫「波兰表示法」),将每个节点写在其子节点前面,顺序自左至右。例如,数学表达式 2 3∗(5 2) 按照前缀表示法可被表示为序列 [ 2 ∗ 3 5 2]。与更常见的中缀表示法 2 3 ∗ (5 2) 相比,前缀序列没有括号、长度更短。在序列内,运算符、函数或变量都由特定 token 来表示,符号位于整数前面。表达式与树之间存在映射关系,同样地,树与前缀序列之间也存在一对一的映射。
生成随机表达式
要想创建训练数据,我们需要生成随机数学表达式。但是,均匀采样具备 n 个内部节点的表达式并不是一项简单的任务。朴素算法(如使用固定概率作为叶节点、一元节点、二元节点的递归方法)倾向于深的树而非宽的树。以下示例展示了研究者想使用相同概率生成的不同树。

计数表达式(COUNTING EXPRESSION)
接下来需要研究所有可能表达式的数量。表达式是基于有限的变量(即文字)、常量、整数和一系列运算符创建得到的,这些运算符可以是简单函数(如 cos 或 exp),也可以更加复杂(如微分或积分)。准确来讲,研究者将问题空间定义为:
至多具备 n 个内部节点的树;p_1 个一元运算符(如 cos、sin、exp、log);p_2 个二元运算符(如 、−、×、pow);L 个叶节点,包含变量(如 x、y、z)、常量(如 e、π)、整数(如 {−10, . . . , 10})。
图 1 展示了不同内部节点数量所对应的二元树数量(C_n)和 unary-binary 树数量(S_n)。研究者还展示了不同运算符和叶节点组合所对应的表达式数量(E_n)。

图 1:不同数量的运算符和叶节点所对应的树和表达式的数量。p_1 和 p_2 分别对应一元运算符和二元运算符的数量,L 对应叶节点数量。最下方的两条曲线对应二元树和 unary-binary 树的数量。最上方两条曲线表示表达式的数量。从该图可以观察到,添加叶节点和二元运算符能够显著扩大问题空间的规模。
万事俱备,只欠数据集
为数学问题和技术定义语法并随机生成表达式后,现在需要为模型构建数据集了。该论文剩余部分主要探讨两个符号数学问题:函数积分和解一阶、二阶常微分方程。
要想训练网络,首先需要包含问题及其对应解的数据集。在完美情况下,研究者想要生成能够代表问题空间的样本,即随机生成待解的积分和微分方程。然而,随机问题的解有时并不存在或者无法轻松推导出来。研究者提出了一些技术,生成包含积分和一阶、二阶常微分方程的大型训练数据集。
积分
研究者提出三种方法来生成函数及其积分。
前向生成(Forward generation,FWD):该方法直接生成具备多达 n 个运算符的随机函数,并通过计算机代数系统计算其积分。系统无法执行积分操作的函数即被舍弃。该方法生成对问题空间子集具备代表性的样本,这些样本可被外部符号数学框架成功求解。
后向生成(Backward generation,BWD):该方法生成随机函数 f,并计算其导数 f',将 (f', f) 对添加到训练集。与积分不同,微分通常是可行的且速度极快,即使是面对非常大的表达式。与前向生成方法相反,后向生成方法不依赖外部符号积分系统。
使用部分积分的后向生成(Backward generation with integration by parts (IBP)):该方法利用部分积分:给出两个随机生成函数 F 和 G,计算各自的导数 f 和 g。如果 fG 已经属于训练集,我们就可以知道其积分,然后计算 Fg 的积分:

该方法可在不依赖外部符号积分系统的情况下生成函数积分,如 x^10 sin(x)。
一阶常微分方程(ODE 1)
如何生成具备解的一阶常微分方程?研究者提出了一种方法。给定一个双变量函数 F(x, y),使方程 F(x, y) = c(c 是常量)的解析解为 y。也就是说,存在双变量函数 f 满足

。对 x 执行微分,得到 ∀x, c:

其中 f_c = x |→ f(x, c)。因此,对于任意常量 c,f_c 都是一阶常微分方程的解:

利用该方法,研究者通过附录中 C 部分介绍的方法生成任意函数 F(x, y),该函数的解析解为 y,并创建了包含微分方程及其解的数据集。
研究者没有生成随机函数 F,而是生成解 f(x, c),并确定它满足的微分方程。如果 f(x, c) 的解析解是 c,则我们计算 F 使 F (x, f(x, c)) = c。通过上述方法,研究者证明,对于任意常量 c,x |→ f(x, c) 都是微分方程 3 的解。最后,对得到的微分方程执行因式分解,并移除方程中的所有正因子。
使用该方法的必要条件是生成解析解为 c 的函数 f(x, c)。由于这里使用的所有运算符和函数都是可逆的,因此确保 c 为解的简单条件是确保 c 在 f(x, c) 树表示的叶节点中仅出现一次。生成恰当 f(x, c) 的直接方式是使用附录中 C 部分介绍的方法采样随机函数 f(x),并将其树表示中的一个叶节点替换成 c。以下示例展示了全过程:

二阶常微分方程(ODE 2)
前面介绍的生成一阶常微分方程的方法也可用于二阶常微分方程,只需要考虑解为 c_2 的三变量函数 f(x, c_1, c_2)。
和之前方法一样,研究者推导出三变量函数 F,使 F (x, f(x, c_1, c_2), c_1) = c_2。对 x 执行微分获得一阶常微分方程:

其中 f_c1,c2 = x |→ f(x, c1, c2)。如果该方程的解为 c_1,则我们可以推断出另一个三变量函数 G 满足:
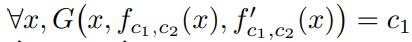
对 x 执行第二次微分,得到以下方程:
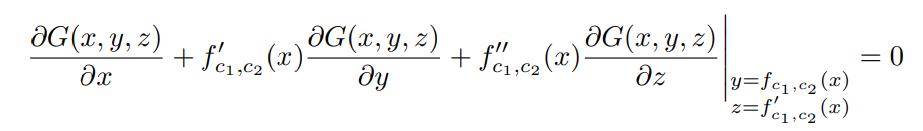
因此,对于任意常量 c_1 和 c_2,f_c1,c2 是二阶常微分方程的解:

通过该方法,研究者创建了二阶常微分方程及其解的对,前提是生成的 f(x, c_1, c_2) 的解为 c_2,对应一阶常微分方程的解为 c_1。
对于 c_1,研究者使用了一个简单的方法,即如果我们不想其解为 c_1,我们只需跳过当前方程即可。尽管简单,但研究者发现在大约一半的场景中,微分方程的解是 c_1。示例如下:

数据集清洗
方程简化:在实践中,研究者简化生成的表达式,以减少训练集中唯一方程的数量,从而缩短序列长度。此外,研究者不想在可以使模型预测 x 5 的情况下,令其预测 x 1 1 1 1 1。
系数简化:在一阶常微分方程中,研究者更改一个变量,将生成的表达式变为另一个等价表达式。研究者对二阶常微分方程也使用了类似的方法,不过二阶方程有两个常量 c_1 和 c_2,因此简化略微复杂一些。
无效表达式:最后,研究者从数据集中删除无效的表达式。如果子树的值不是有限实数(如−∞、 ∞或复数),则丢弃该表达式。
实验
数据集
表 1 展示了数据集统计情况。如前所述,研究者观察到后向生成方法生成的导数(即输入)比前向生成器要长得多,详见附录中 E 部分内容。
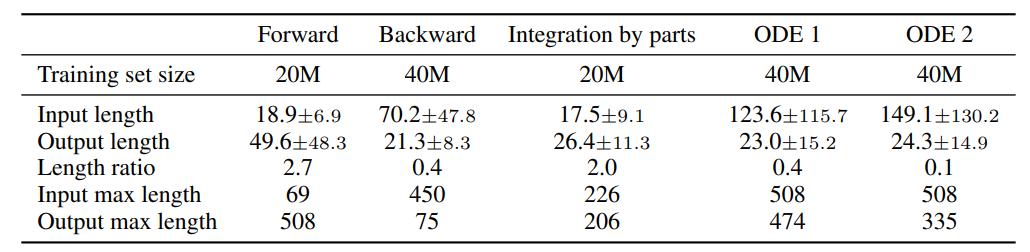
表 1:不同数据集的训练集大小和表达式长度。FWD 和 IBP 生成样本的输出比输入长,而 BWD 方法生成样本的输出比输入短。和 BWD 类似,ODE 生成器输出的解也比方程短。
模型
对于所有实验,研究者训练 seq2seq 模型来预测给定问题的解,即预测给定函数的原函数或预测给定微分方程的解。研究者使用 transformer 模型 (Vaswani et al., 2017),该模型有 8 个注意力头、6 个层,维度为 512。
研究者使用 Adam 优化器训练模型,学习率为 10^−4。研究者移除长度超过 512 个 token 的表达式,以每批次 256 个方程来训练模型。
在推断过程中,表达式通过集束搜索来生成,并使用早停法。研究者将集束中所有假设的对数似然分数按其序列长度进行归一化。这里使用的集束宽度为 1(即贪婪解码)、10 和 50。
在解码过程中,模型不可避免地会生成无效的前缀表达式。研究者发现模型生成结果几乎总是无效的,于是决定不使用任何常量。当模型生成无效表达式时,研究者仅将其作为错误解并忽略它。
评估
在每个 epoch 结束时,研究者评估模型预测给定方程解的能力。但是,研究者可以通过对比生成表达式及其参考解,轻松核对模型的正确性。
因此,研究者考虑集束中的所有假设,而不只是最高分的假设。研究者核实每个假设的正确性,如果其中一个正确的话,则模型对输入方程成功求解。因此,「Beam size 10」的结果表示,集束中 10 个假设里至少有一个是正确的。
结果
下表 2 展示了模型对函数积分和微分方程求解的准确率。

表 2:模型对函数积分和微分方程求解的准确率。所有结果均基于包含 5000 个方程的留出测试集。对于微分方程,使用集束搜索解码显著提高了模型准确率。
下表 3 展示了不同集束大小时模型的准确率,此处 Mathematica 有 30 秒的超时延迟。

表 3:该研究提出的模型与 Mathematica、Maple 和 Matlab 在包含 500 个方程的测试集上的性能对比情况。此处,Mathematica 处理每个方程时有 30 秒的超时延迟。对于给定方程,该研究提出的模型通常在不到一秒的时间内即可找出解。
下表 4 展示了该研究提出模型能解而 Mathematica 和 Matlab 不能解的函数示例:

表 4:该研究提出模型能解而 Mathematica 和 Matlab 不能解的函数示例。对于每个方程,该研究提出的模型使用贪婪解码找出有效解。
下表 5 是模型对方程返回的 top 10 假设。研究者发现,所有生成结果实际上都是有效解,尽管它们的表达式迥然不同。

表 5:通过集束搜索方法,模型对一阶常微分方程

返回的 top 10 生成结果。
下表 6 对比了使用不同训练数据组合训练得到的 4 个模型在 FWD、BWD 和 IBP 测试集上的准确率情况。

表 6:该研究提出的模型对函数积分求解的准确率。FWD 训练的模型在对来自 BWD 数据集的函数执行积分时性能较差。
FWD 训练模型有时可对 SymPy 无法求积分的函数执行积分操作,下表 7 展示了此类函数的示例:

表 7:FWD 训练模型可求积分而 SymPy 不可求积分的函数/积分示例。尽管 FWD 模型仅在 SymPy 可求积分函数的子集上训练,但它可以泛化至 SymPy 不可求积分的函数。
下表 8 展示了超时值对 Mathematica 准确率的影响。增加超时延迟的值可提高准确率。

表 8:在不同超时值情况下,Mathematica 对 500 个函数求积分的准确率。随着超时延迟值增大,超时次数下降,因而失败率下降。在 3 分钟极限情况下,超时次数仅带来 10% 的失败。因此,没有超时的准确率不会超过 86.2%。
,




