两异面直线间的距离怎么求（求异面直线的距离）

已知正方体ABCD

的棱长为1，求异面直线与AC的距离。

一、直接利用定义求解

作出异面直线的公垂线段。

如图1，取AD中点M，连

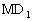
、MB分别交、AC于E、F，连，由平面几何知识，易证

，

，

，则

。

由

，

得⊥平面

，则

，同理AC⊥，所以，EF⊥，EF⊥AC，即EF为异面直线与AC的距离，故有EF=

。

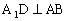
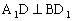
二、转化为线面距离求解

将线线距离问题转化为线面距离问题来解。

如图2，连、

，则AC∥平面。设AC、BD交于O，、

交于

，连

，作OE⊥于E，由⊥平面

知

，故OE⊥平面。

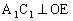
所以OE为异面直线与AC的距离。

在

△

中，

，则

。

所以异面直线与AC的距离为。

三、转化为面面距离求解

将线线距离问题转化为面面距离问题来解。

如图3，连

、

、、

、，易知平面

，则异面直线与AC的距离就是平面与平面

的距离，易证⊥

、⊥平面，且被平面和平面三等分，又

。

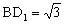
所以异面直线与AC的距离为。

四、构造函数求解

选取恰当的自变量构造函数，即可利用函数的最小值求得异面直线间的距离。

如图4，在上任取一点E，作EM⊥AD于M，再作MF⊥AC于F，连EF，则∠EMF=

。

设MD=

，则ME=，AM

，在

中，∠FAM=

，则

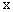
所以

，

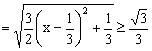
当且仅当

时，EF取最小值。

所以异面直线与AC的距离为。

五、利用体积变换求解

将异面直线的距离转化为锥体的高，然后利用体积公式求之。

如图5，连、

、

，则∥平面

，设异面直线与AC的距离为

，则D到平面的距离也为。

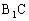
易知

，

。

由

，

得

。

所以

，则

。

所以异面直线与AC的距离为。

六、利用向量求解

如图6，AB为异面直线

、

的公垂线段，

为直线AB的方向向量，E、F分别为直线、上的任意一点，则

。

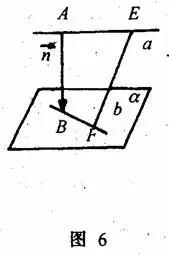
证明：显然

=

，

，

。

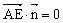
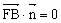
所以

，

所以

，

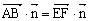
所以

，即

，

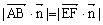
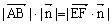
所以

。

把上述结论作为公式来用，即可巧妙地求出某些问题中的异面直线间的距离。

建立如图7所示的空间直角坐标系，易知

，

=（-1，1，0），

（-1，0，0）。

设异面直线、AC的公垂线的方向向量为

，由

，

，得

解得

故可取

。

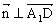
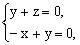
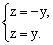
所以异面直线与AC的距离为

。

,