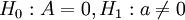1、什么是环比
环比发展速度是报告期水平与前一时期水平之比,表明现象逐期的发展速度。如计算一年内各月与前一个月对比,即2月比1月,3月比2月,4月比3月 ……12月比11月,说明逐月的发展程度。
发展速度由于采用基期的不同,可分为同比发展速度、环比发展速度和定基发展速度。均用百分数或倍数表示。环比分为日环比、周环比、月环比和年环比。
环比计算公式
环比增长速度=(本期数-上期数)/上期数*100%
环比分析
通过环比分析可消除年报缺陷给投资者造成的误导。大家知道,年报的同比分析就是用报告期数据与上期或以往几个年报数据进行对比。它可以告诉投资者在过去一年或几年中,上市公司的业绩是增长还是滑坡。但是,年报的同比分析不能揭示公司最近6个月的业绩增长变动情况,而这一点对投资决策更富有指导意义。
所谓环比分析,就年报而言,就是将下半年业绩数据与上半年业绩数据做比较。其中,下半年业绩数据可以用全年数减去中期数获得,将得数除以中期数,再乘以百分之百,便得出报告期环比增减变动比率或幅度。
例如
某公司2000年全年主营业务收入为395364万元,2000年中期主营业务收入仅为266768万元,二者相减得出下半年主营业务收入为128596万元,再用128596万元除以266768万元,乘以百分之百,便得出该公司报告期主营业务收入环比大幅滑坡51.80%的分析结果。通过环比分析可消除年报缺陷给投资者造成的误导。
2、什么是因素估算法
因素估算法是根据客观现象内部各因素之间的联系,从已知因素的统计信息来推算未知因素指标的方法。客观现象的某项指标有可能分解为若干个影响因素,各影响因素的指标及其变动的乘积或商等于该项指标的总量及其变动。
因素估算法举例
例如:
-
工业总产值=职工人数×全员劳动生产率;
-
商品零售额指数=商品零售量指数×零售价格指数;
-
货币购买力指数=1/职工生活费指数;等等。
根据上列这些因素之间的联系,已知某项因素的统计信息,就可推算未知因素的指标。
设:某地区商品零售额指数为126%。零售价格指数为105%,职工生活费指数为111%。
要求:应用因素估算法推算商品零售量指数和货币购买力指数。
-
商品零售指数=商品零售额指数/商品零售价格指数=126%/105%=120%
-
货币购买力指数=1/职工生活费指数=1/111%=90%
3、什么是秩和检验
秩和检验方法最早是由维尔克松提出,叫维尔克松两样本检验法。后来曼—惠特尼将其应用到两样本容量不等(

)的情况,因而又称为曼—惠特尼U检验。这种方法主要用于比较两个独立样本的差异。
1、假设中的等价问题
设有两个连续型总体, 它们的概率密度函数分别为:
f1(x),f2(x)(均为未知)
已知f1(x) = f2(x − a),a为末知常数,要检验的各假设为:
H0:A = 0,H1:a < 0.
H0:A = 0,H1:a > 0.
.
设两个总体的均值存在,分别记为μ1,μ2,由于f1,f2最多只差一平移,则有μ2 = μ1 − a。此时, 上述各假设分别等价于:
H0:μ1 = μ2,H1:μ1 < μ2
H0:μ1 = μ2,H1:μ1 > μ2
2、秩的定义
设X为一总体,将容量为n的样本观察值按自小到大的次序编号排列成x(1) < x(2) < Λ < x(n),称x(i)的足标i为x(i)的秩,i = 1,2,Λ,n。
例如:某施行团人员的行李重量数据如表:
重量(kg)
34
39
41
28
33
写出重量33的秩。
因为28<33<34<39<41,故33的秩为2。
特殊情况:
如果在排列大小时出现了相同大小的观察值, 则其秩的定义为足标的平均值。
例如: 抽得的样本观察值按次序排成0,1,1,1,2,3,3,
则3个1的秩均为
,
两个3的秩均为
.
3、秩和的定义
现设1,2两总体分别抽取容量为n1,n2的样本,且设两样本独立。这里总假定
。
我们将这n1 n2个观察值放在一起,按自小到大的次序排列,求出每个观察值的秩,然后将属于第1个总体的样本观察值的秩相加,其和记为R1,称为第1样本的秩和,其余观察值的秩的总和记作R2,称为第2样本的秩和。
显然,R1和R2是离散型随机变量,且有
4、秩和检验法的定义
秩和检验是一种非参数检验法, 它是一种用样本秩来代替样本值的检验法。
用秩和检验可以检验两个总体的分布函数是否相等的问题
4、什么是游程检验
游程检验亦称“连贯检验”,是根据样本标志表现排列所形成的游程的多少进行判断的检验方法。
设某样本n=12人的标志表现为男、女,有以下三种排列。
(i) 男\男,女\女\女,男,女\女,男\男\男\男
(ii) 男\男\男\男\男\男\男,女\女\女\女\女
(iii)男,女,男,女,男,女,男,女,男,女,男\男
连续出现男或女的区段称为游程。
每个游程包含的个数为游程长度。以r表示序列中游程的个数:
(i)r=5, (ii)r=2, (iii)r=11
可以看出,(i)是随机性序列;(ii)(iii)是非随机性序列,所以,可以用游程的个数来检验样本的随机性,或总体的分布特征。
游程检验方法
1、检验总体分布是否相同
将从两个总体中独立抽取的两个样本的观察值混合后,观察游程个数,进行比较。
2、检验样本的随机性
将取自某一总体的样本的观察值按从小到大顺序排列,找出中位数(或平均数),分为大于中位数的小于中位数的两个部分。用上下交错形成的游程个数来检验样本是否是随机的。
3、检验规则(小样本。n<20)
应用表La和Lb,(α=0.05,r为临界值)
1)单侧检验:
观察到的游程个数r0≤临界值(La表)或r0≥临界值(Lb表),否定H0;反之,接受H0。
2)双侧检验:
观察到的游程个数r0
r(La)<ro<r(Lb),接受Ho
下限 上限
反之,拒绝H0
4、大样本(n1或n2大于20)
游程个数r近似正态分布,检验统计量
其中:
5、什么是指数平滑法
指数平滑法是布朗(Robert G..Brown)所提出,布朗(Robert G..Brown)认为时间序列的态势具有稳定性或规则性,所以时间序列可被合理地顺势推延;他认为最近的过去态势,在某种程度上会持续到最近的未来,所以将较大的权数放在最近的资料。
指数平滑法是生产预测中常用的一种方法。也用于中短期经济发展趋势预测,所有预测方法中,指数平滑是用得最多的一种。简单的全期平均法是对时间数列的过去数据一个不漏地全部加以同等利用;移动平均法则不考虑较远期的数据,并在加权移动平均法中给予近期资料更大的权重;而指数平滑法则兼容了全期平均和移动平均所长,不舍弃过去的数据,但是仅给予逐渐减弱的影响程度,即随着数据的远离,赋予逐渐收敛为零的权数。
也就是说指数平滑法是在移动平均法基础上发展起来的一种时间序列分析预测法,它是通过计算指数平滑值,配合一定的时间序列预测模型对现象的未来进行预测。其原理是任一期的指数平滑值都是本期实际观察值与前一期指数平滑值的加权平均。
指数平滑法的基本公式
指数平滑法的基本公式是:St=ayt (1-a)St-1 式中,
St--时间t的平滑值;
yt--时间t的实际值;
St-1--时间t-1的实际值;
a--平滑常数,其取值范围为[0,1];
由该公式可知:
1.St是yt和 St-1的加权算数平均数,随着a取值的大小变化,决定yt和 St-1对St的影响程度,当a取1时,St= yt;当a取0时,St= St-1。
2.St具有逐期追溯性质,可探源至St-t 1为止,包括全部数据。其过程中,平滑常数以指数形式递减,故称之为指数平滑法。指数平滑常数取值至关重要。平滑常数决定了平滑水平以及对预测值与实际结果之间差异的响应速度。平滑常数a越接近于1,远期实际值对本期平滑值的下降越迅速;平滑常数a越接近于 0,远期实际值对本期平滑值影响程度的下降越缓慢。由此,当时间数列相对平稳时,可取较大的a;当时间数列波动较大时,应取较小的a,以不忽略远期实际值的影响。生产预测中,平滑常数的值取决于产品本身和管理者对良好响应率内涵的理解。
3.尽管St包含有全期数据的影响,但实际计算时,仅需要两个数值,即yt和 St-1,再加上一个常数a,这就使指数滑动平均具逐期递推性质,从而给预测带来了极大的方便。
4.根据公式S1=ay1 (1-a)S0,当欲用指数平滑法时才开始收集数据,则不存在y0。无从产生S0,自然无法据指数平滑公式求出S1,指数平滑法定义S1为初始值。初始值的确定也是指数平滑过程的一个重要条件。
如果能够找到y1以前的历史资料,那么,初始值S1的确定是不成问题的。数据较少时可用全期平均、移动平均法;数据较多时,可用最小二乘法。但不能使用指数平滑法本身确定初始值,因为数据必会枯竭。
如果仅有从y1开始的数据,那么确定初始值的方法有:
1)取S1等于y1;
2)待积累若干数据后,取S1等于前面若干数据的简单算术平均数,如:S1=(y1 y2 y3)/3等等。
指数平滑的预测公式
据平滑次数不同,指数平滑法分为:一次指数平滑法、二次指数平滑法和三次指数平滑法等。
(一) 一次指数平滑预测
当时间数列无明显的趋势变化,可用一次指数平滑预测。其预测公式为:
yt 1'=ayt (1-a)yt' 式中,
yt 1'--t 1期的预测值,即本期(t期)的平滑值St ;
yt--t期的实际值;
yt'--t期的预测值,即上期的平滑值St-1 。
该公式又可以写作:yt 1'=yt' a(yt- yt')。可见,下期预测值又是本期预测值与以a为折扣的本期实际值与预测值误差之和。
(二) 二次指数平滑预测
二次指数平滑是对一次指数平滑的再平滑。它适用于具线性趋势的时间数列。其预测公式为:
yt m=(2 am/(1-a))yt'-(1 am/(1-a))yt=(2yt'-yt) m(yt'-yt) a/(1-a)
式中,yt= ayt-1' (1-a)yt-1
显然,二次指数平滑是一直线方程,其截距为:(2yt'-yt),斜率为:(yt'-yt) a/(1-a),自变量为预测天数。
(三) 三次指数平滑预测
三次指数平滑预测是二次平滑基础上的再平滑。其预测公式是:
yt m=(3yt'-3yt yt) [(6-5a)yt'-(10-8a)yt (4-3a)yt]*am/2(1-a)2 (yt'-2yt yt')*a2m2/2(1-a)2
式中,yt=ayt-1 (1-a)yt-1
它们的基本思想都是:预测值是以前观测值的加权和,且对不同的数据给予不同的权,新数据给较大的权,旧数据给较小的权。
指数平滑法的趋势调整
一段时间内收集到的数据所呈现的上升或下降趋势将导致指数预测滞后于实际需求。通过趋势调整,添加趋势修正值,可以在一定程度上改进指数平滑预测结果。调整后的指数平滑法的公式为:
包含趋势预测(YITt)=新预测(Yt) 趋势校正(Tt)
进行趋势调整的指数平滑预测有三个步骤:
1、 利用前面介绍的方法计算第t期的简单指数平滑预测(Yt);
2、 计算趋势。其公式为: Tt=(1-b)Tt-1 b(Yt-Yt-1)其中,
Tt=第t期经过平滑的趋势;
Tt-1=第t期上期经过平滑的趋势;
b=选择的趋势平滑系数;
Yt=对第t期简单指数平滑预测;
Yt-1=对第t期上期简单指数平滑预测。
3、计算趋势调整后的指数平滑预测值(YITt)。计算公式为:YITt=Yt Tt。
6、什么是F分布
F分布是以统计学家R.A.Fisher姓氏的第一个字母命名的.
F分布定义为:设X、Y为两个独立的随机变量,X服从自由度为k1的>2分布,Y服从自由度为k2的>2 分布,这2 个独立的>2分布被各自的自由度除以后的比率这一统计量的分布。即: 上式F服从第一自由度为k1,第二自由度为k2的F分布
F分布的性质
1、它是一种非对称分布;
2、它有两个自由度,即n1 -1和n2-1,相应的分布记为F( n1 –1, n2-1), n1 –1通常称为分子自由度, n2-1通常称为分母自由度;
3、F分布是一个以自由度n1 –1和n2-1为参数的分布族,不同的自由度决定了F 分布的形状。
4、F分布的倒数性质:Fα,df1,df2=1/F1-α,df1,df2
7、什么是T分布(学生分布)
t分布(t-distribution)
(一)u分布
正态分布(normal distribution)是数理统计中的一种重要的理论分布 ,是许多统计方法的理论基础。正态分布有两个参数,μ和σ,决定了正态分布的位置和形态。为了应用方便,常将一般的正态变量X通过u变换[(X-μ)/σ]转化成标准正态变量u,以使原来各种形态的正态分布都转换为μ=0,σ=1的标准正态分布(standard normal distribution),亦称u分布。
根据中心极限定理,通过上述的抽样模拟试验表明,在正态分布总体中以固定n(本次试验n=10)抽取若干个样本时,样本均数的分布仍服从正态分布,即N(μ,σ)。所以,对样本均数的分布进行u变换[],也可变换为标准正态分布N (0,1)
(二)t分布
由于在实际工作中,往往σ是未知的,常用s作为σ的估计值,为了与u变换区别,称为t变换t=,统计量t 值的分布称为t分布。
t分布特征
1.以0为中心,左右对称的单峰分布;
2.t分布是一簇曲线,其形态变化与n(确切地说与自由度ν)大小有关。自由度ν越小,t分布曲线越低平;自由度ν越大,t分布曲线越接近标准正态分布(u分布)曲线。
对应于每一个自由度ν,就有一条t分布曲线,每条曲线都有其曲线下统计量t的分布规律,计算较复杂。
学生的t分布(或也t分布) ,在概率统计,是一个概率分布出现在的问题,估计是指一个通常的分布式人口时,样本大小是小。它的基础是受欢迎的学生的T -测试统计的意义之间的差异两个范例手段,为置信区间之间的差额二人口的手段。学生的t分布是一种特殊情况,对一般性的双曲分布。
推导了t分布是由William Gosset西利高大伟于1908年首次出版,而他在工作健力士啤酒厂在都柏林。他被禁止以他他个人的名义出版,因此,该文件是根据书面笔名学生"student"。 t检验和相关的理论,成为著名的透过工作的RA余志稳,谁的所谓分配“学生的分配” (student's t)。
t分布情况出现时(如在几乎所有实际的统计工作)的人口标准偏差是未知的,并要估算,从数据。教科书问题的处理标准偏差,因为如果它被称为是两类: ( 1 )那些在该样本规模是如此之大的一个可处理的数据为基础估计的差异,就好像它一定的,和( 2 )这些说明数学推理,在其中的问题,估计标准偏差是暂时忽略,因为这不是一点,作者或导师是当时的解释。
t分布的概述及其历史
在概率论和统计学中,学生t-分布(Student's t-distribution)应用在当对呈正态分布的母群体的均值进行估计。它是对两个样本均值差异进行显著性测试的学生t测定的基础。t检定改进了Z检定(en:Z-test),不论样本数量大或小皆可应用。在样本数量大(超过120等)时,可以应用Z检定,但Z检定用在小的样本会产生很大的误差,因此样本很小的情况下得改用学生t检定。在数据有三组以上时,因为误差无法压低,此时可以用变异数分析代替学生t检定。
当母群体的标准差是未知的但却又需要估计时,我们可以运用学生t-分布。
学生t-分布可简称为t分布。其推导由威廉•戈塞于1908年首先发表,当时他还在都柏林的健力士酿酒厂工作。因为不能以他本人的名义发表,所以论文使用了学生(Student)这一笔名。之后t检验以及相关理论经由罗纳德•费雪的工作发扬光大,而正是他将此分布称为学生分布。
8、什么是二项分布
二项分布(binomial distribution)是一个离散型概率分布。它描述n个独立的伯努利试验的成功次数。此伯努利试验成功概率为p。一个分布X如果服从次数为n,成功概率为p的二项分布,记作:X˜B(n,p)
二项分布的概率质量函数(Probability Mass Function,PMF)如下:
其中
数学期望为np。
变异数或方差为npq=np(1-p)。
9、什么是综合评价法?
运用多个指标对多个参评单位进行评价的方法,称为多变量综合评价方法,或简称综合评价方法。其基本思想是将多个指标转化为一个能够反映综合情况的指标来进行评价。如不同国家经济实力,不同地区社会发展水平,小康生活水平达标进程,企业经济效益评价等,都可以应用这种方法。
综合评价方法的种类
现代综合评价方法包括主成分分析法、数据包络分析法、模糊评价法等。
(1)主成分分析法。主成分分析是多元统计分析的一个分支。是将其分量相关的原随机向量,借助于一个正交变换,转化成其分量不相关的新随机向量,并以方差作为信息量的测度,对新随机向量进行降维处理。再通过构造适当的价值函数,进一步做系统转化。
(2)数据包络分析法。它是创建人以其名字命名的DEA模型——C2R模型。DEA法不仅可对同一类型各决策单元的相对有效性做出评价与排序,而且还可进一步分析各决策单元非DE有效的原因及其改进方向,从而为决策者提供重要的管理决策信息。
(3)模糊评价法。模糊评价法奠基于模糊数学。它不仅可对评价对象按综合分值的大小进行评价和排序,而且还可根据模糊评价集上的值按最大隶属度原则去评定对象的等级。
综合评价法的特点
综合评价法的特点表现为:
(1)评价过程不是逐个指标顺次完成的,而是通过一些特殊方法将多个指标的评价同时完成的;
(2)在综合评价过程中,一般要根据指标的重要性进行加权处理;
(3)评价结果不再是具有具体含义的统计指标,而是以指数或分值表示参评单位"综合状况"的排序。
综合评价法的要素
构成综合评价的要素主要有:
1.评价者。评价者可以是某个人或某团体。评价目的的给定、评价指标的建立、评价模型的选择、权重系数的确定都与评价者有关。因此,评价者在评价过程的作用是不可轻视的。
2.被评价对象。随着综合评价技术理论的开展与实践活动,评价的领域也从最初的各行各业经济统计综合评价拓展到后来的技术水平、生活质量、小康水平、社会发展、环境质量、竞争能力、综合国力、绩效考评等方面。这些都能构成被评价对象。
3.评价指标。评价指标体系是从多个视角和层次反映特定评价客体数量规模与数量水平的。它是一个“具体一抽象一具体”的辩证逻辑思维过程,是人们对现象总体数量特征的认识逐步深化、求精、完善、系统化的过程。
4.权重系数。相对于某种评价目的来说,评价指标相对重要性是不同的。权重系数确定的合理与否,关系到综合评价结果的可信程度。
5.综合评价模型。所谓多指标综合评价,就是指通过一定的数学模型将多个评价指标值“合成”为一个整体性的综合评价值。
综合评价法的步骤
1、确定综合评价指标体系,这是综合评价的基础和依据。
2、收集数据,并对不同计量单位的指标数据进行同度量处理。
3、确定指标体系中各指标的权数,以保证评价的科学性。
4、对经过处理后的指标在进行汇总计算出综合评价指数或综合评价分值。
5、根据评价指数或分值对参评单位进行排序,并由此得出结论。
综合评价分析指标值的计算方法
主要有打分综合法、打分排队法、综合指数法、功效系数法等。
10、什么是泊松分布
泊松分布(Poisson distribution),台译卜瓦松分布,是一种统计与概率学里常见到的离散机率分布(discrete probability distribution),由法国数学家西莫恩·德尼·泊松(Siméon-Denis Poisson)在1838年时发表。 泊松分布的概率密度函数为: P(X=k)=\frac{e^{-\lambda}\lambda^k}{k!} 泊松分布的参数λ是单位时间(或单位面积)内随机事件的平均发生率。 泊松分布适合于描述单位时间内随机事件发生的次数。如某一服务设施在一定时间内到达的人数,电话交换机接到呼叫的次数,汽车站台的候客人数,机器出现的故障数,自然灾害发生的次数等等。
(Poisson distribution),-{zh-cn:台译卜瓦松分布;zh-tw:也译为布瓦松分布,布阿松分布,波以松分布等}-,是一种统计与概率学里常见到的离散机率分布(discrete probability distribution),由法国数学家(Siméon-Denis Poisson)在1838年时发表。
泊松分布的概率密度函数为:
P(X=k)=\frac{e^{-\lambda}\lambda^k}{k!}
泊松分布的参数λ是单位时间(或单位面积)内随机事件的平均发生率。
11、什么是因素估算法
因素估算法是根据客观现象内部各因素之间的联系,从已知因素的统计信息来推算未知因素指标的方法。客观现象的某项指标有可能分解为若干个影响因素,各影响因素的指标及其变动的乘积或商等于该项指标的总量及其变动。
因素估算法举例
例如:
工业总产值=职工人数×全员劳动生产率;
商品零售额指数=商品零售量指数×零售价格指数;
货币购买力指数=1/职工生活费指数;等等。
根据上列这些因素之间的联系,已知某项因素的统计信息,就可推算未知因素的指标。
设:某地区商品零售额指数为126%。零售价格指数为105%,职工生活费指数为111%。
要求:应用因素估算法推算商品零售量指数和货币购买力指数。
商品零售指数=商品零售额指数/商品零售价格指数=126%/105%=120%
货币购买力指数=1/职工生活费指数=1/111%=90%
12、什么是秩和检验
秩和检验方法最早是由维尔克松提出,叫维尔克松两样本检验法。后来曼—惠特尼将其应用到两样本容量不等(
)的情况,因而又称为曼—惠特尼U检验。这种方法主要用于比较两个独立样本的差异。
1、假设中的等价问题
设有两个连续型总体, 它们的概率密度函数分别为:
f1(x),f2(x)(均为未知)
已知f1(x) = f2(x − a),a为末知常数,要检验的各假设为:
H0:A = 0,H1:a < 0.
H0:A = 0,H1:a > 0.
.
设两个总体的均值存在,分别记为μ1,μ2,由于f1,f2最多只差一平移,则有μ2 = μ1 − a。此时, 上述各假设分别等价于:
H0:μ1 = μ2,H1:μ1 < μ2
H0:μ1 = μ2,H1:μ1 > μ2
2、秩的定义
设X为一总体,将容量为n的样本观察值按自小到大的次序编号排列成x(1) < x(2) < Λ < x(n),称x(i)的足标i为x(i)的秩,i = 1,2,Λ,n。
例如:某施行团人员的行李重量数据如表:
重量(kg)
34
39
41
28
33
写出重量33的秩。
因为28<33<34<39<41,故33的秩为2。
特殊情况:
如果在排列大小时出现了相同大小的观察值, 则其秩的定义为足标的平均值。
例如: 抽得的样本观察值按次序排成0,1,1,1,2,3,3,
则3个1的秩均为
,
两个3的秩均为
.
3、秩和的定义
现设1,2两总体分别抽取容量为n1,n2的样本,且设两样本独立。这里总假定
。
我们将这n1 n2个观察值放在一起,按自小到大的次序排列,求出每个观察值的秩,然后将属于第1个总体的样本观察值的秩相加,其和记为R1,称为第1样本的秩和,其余观察值的秩的总和记作R2,称为第2样本的秩和。
显然,R1和R2是离散型随机变量,且有
4、秩和检验法的定义
秩和检验是一种非参数检验法, 它是一种用样本秩来代替样本值的检验法。
用秩和检验可以检验两个总体的分布函数是否相等的问题
13、什么是游程检验
游程检验亦称“连贯检验”,是根据样本标志表现排列所形成的游程的多少进行判断的检验方法。
设某样本n=12人的标志表现为男、女,有以下三种排列。
(i) 男\男,女\女\女,男,女\女,男\男\男\男
(ii) 男\男\男\男\男\男\男,女\女\女\女\女
(iii)男,女,男,女,男,女,男,女,男,女,男\男
连续出现男或女的区段称为游程。
每个游程包含的个数为游程长度。以r表示序列中游程的个数:
(i)r=5, (ii)r=2, (iii)r=11
可以看出,(i)是随机性序列;(ii)(iii)是非随机性序列,所以,可以用游程的个数来检验样本的随机性,或总体的分布特征。
游程检验方法
1、检验总体分布是否相同
将从两个总体中独立抽取的两个样本的观察值混合后,观察游程个数,进行比较。
2、检验样本的随机性
将取自某一总体的样本的观察值按从小到大顺序排列,找出中位数(或平均数),分为大于中位数的小于中位数的两个部分。用上下交错形成的游程个数来检验样本是否是随机的。
3、检验规则(小样本。n<20)
应用表La和Lb,(α=0.05,r为临界值)
1)单侧检验:
观察到的游程个数r0≤临界值(La表)或r0≥临界值(Lb表),否定H0;反之,接受H0。
2)双侧检验:
观察到的游程个数r0
r(La)<ro<r(Lb),接受Ho
下限 上限
反之,拒绝H0
4、大样本(n1或n2大于20)
游程个数r近似正态分布,检验统计量
其中:
14、什么是指数平滑法
指数平滑法是布朗(Robert G..Brown)所提出,布朗(Robert G..Brown)认为时间序列的态势具有稳定性或规则性,所以时间序列可被合理地顺势推延;他认为最近的过去态势,在某种程度上会持续到最近的未来,所以将较大的权数放在最近的资料。
指数平滑法是生产预测中常用的一种方法。也用于中短期经济发展趋势预测,所有预测方法中,指数平滑是用得最多的一种。简单的全期平均法是对时间数列的过去数据一个不漏地全部加以同等利用;移动平均法则不考虑较远期的数据,并在加权移动平均法中给予近期资料更大的权重;而指数平滑法则兼容了全期平均和移动平均所长,不舍弃过去的数据,但是仅给予逐渐减弱的影响程度,即随着数据的远离,赋予逐渐收敛为零的权数。
也就是说指数平滑法是在移动平均法基础上发展起来的一种时间序列分析预测法,它是通过计算指数平滑值,配合一定的时间序列预测模型对现象的未来进行预测。其原理是任一期的指数平滑值都是本期实际观察值与前一期指数平滑值的加权平均。
指数平滑法的基本公式
指数平滑法的基本公式是:St=ayt (1-a)St-1 式中,
St--时间t的平滑值;
yt--时间t的实际值;
St-1--时间t-1的实际值;
a--平滑常数,其取值范围为[0,1];
由该公式可知:
1.St是yt和 St-1的加权算数平均数,随着a取值的大小变化,决定yt和 St-1对St的影响程度,当a取1时,St= yt;当a取0时,St= St-1。
2.St具有逐期追溯性质,可探源至St-t 1为止,包括全部数据。其过程中,平滑常数以指数形式递减,故称之为指数平滑法。指数平滑常数取值至关重要。平滑常数决定了平滑水平以及对预测值与实际结果之间差异的响应速度。平滑常数a越接近于1,远期实际值对本期平滑值的下降越迅速;平滑常数a越接近于 0,远期实际值对本期平滑值影响程度的下降越缓慢。由此,当时间数列相对平稳时,可取较大的a;当时间数列波动较大时,应取较小的a,以不忽略远期实际值的影响。生产预测中,平滑常数的值取决于产品本身和管理者对良好响应率内涵的理解。
3.尽管St包含有全期数据的影响,但实际计算时,仅需要两个数值,即yt和 St-1,再加上一个常数a,这就使指数滑动平均具逐期递推性质,从而给预测带来了极大的方便。
4.根据公式S1=ay1 (1-a)S0,当欲用指数平滑法时才开始收集数据,则不存在y0。无从产生S0,自然无法据指数平滑公式求出S1,指数平滑法定义S1为初始值。初始值的确定也是指数平滑过程的一个重要条件。
如果能够找到y1以前的历史资料,那么,初始值S1的确定是不成问题的。数据较少时可用全期平均、移动平均法;数据较多时,可用最小二乘法。但不能使用指数平滑法本身确定初始值,因为数据必会枯竭。
如果仅有从y1开始的数据,那么确定初始值的方法有:
1)取S1等于y1;
2)待积累若干数据后,取S1等于前面若干数据的简单算术平均数,如:S1=(y1 y2 y3)/3等等。
指数平滑的预测公式
据平滑次数不同,指数平滑法分为:一次指数平滑法、二次指数平滑法和三次指数平滑法等。
(一) 一次指数平滑预测
当时间数列无明显的趋势变化,可用一次指数平滑预测。其预测公式为:
yt 1'=ayt (1-a)yt' 式中,
yt 1'--t 1期的预测值,即本期(t期)的平滑值St ;
yt--t期的实际值;
yt'--t期的预测值,即上期的平滑值St-1 。
该公式又可以写作:yt 1'=yt' a(yt- yt')。可见,下期预测值又是本期预测值与以a为折扣的本期实际值与预测值误差之和。
(二) 二次指数平滑预测
二次指数平滑是对一次指数平滑的再平滑。它适用于具线性趋势的时间数列。其预测公式为:
yt m=(2 am/(1-a))yt'-(1 am/(1-a))yt=(2yt'-yt) m(yt'-yt) a/(1-a)
式中,yt= ayt-1' (1-a)yt-1
显然,二次指数平滑是一直线方程,其截距为:(2yt'-yt),斜率为:(yt'-yt) a/(1-a),自变量为预测天数。
(三) 三次指数平滑预测
三次指数平滑预测是二次平滑基础上的再平滑。其预测公式是:
yt m=(3yt'-3yt yt) [(6-5a)yt'-(10-8a)yt (4-3a)yt]*am/2(1-a)2 (yt'-2yt yt')*a2m2/2(1-a)2
式中,yt=ayt-1 (1-a)yt-1
它们的基本思想都是:预测值是以前观测值的加权和,且对不同的数据给予不同的权,新数据给较大的权,旧数据给较小的权。
指数平滑法的趋势调整
一段时间内收集到的数据所呈现的上升或下降趋势将导致指数预测滞后于实际需求。通过趋势调整,添加趋势修正值,可以在一定程度上改进指数平滑预测结果。调整后的指数平滑法的公式为:
包含趋势预测(YITt)=新预测(Yt) 趋势校正(Tt)
进行趋势调整的指数平滑预测有三个步骤:
1、 利用前面介绍的方法计算第t期的简单指数平滑预测(Yt);
2、 计算趋势。其公式为: Tt=(1-b)Tt-1 b(Yt-Yt-1)其中,
Tt=第t期经过平滑的趋势;
Tt-1=第t期上期经过平滑的趋势;
b=选择的趋势平滑系数;
Yt=对第t期简单指数平滑预测;
Yt-1=对第t期上期简单指数平滑预测。
3、计算趋势调整后的指数平滑预测值(YITt)。计算公式为:YITt=Yt Tt。
15、什么是二项分布
二项分布(binomial distribution)是一个离散型概率分布。它描述n个独立的伯努利试验的成功次数。此伯努利试验成功概率为p。一个分布X如果服从次数为n,成功概率为p的二项分布,记作:X˜B(n,p)
二项分布的概率质量函数(Probability Mass Function,PMF)如下:
其中
数学期望为np。
变异数或方差为npq=np(1-p)。
16、什么是综合评价法?
运用多个指标对多个参评单位进行评价的方法,称为多变量综合评价方法,或简称综合评价方法。其基本思想是将多个指标转化为一个能够反映综合情况的指标来进行评价。如不同国家经济实力,不同地区社会发展水平,小康生活水平达标进程,企业经济效益评价等,都可以应用这种方法。
综合评价方法的种类
现代综合评价方法包括主成分分析法、数据包络分析法、模糊评价法等。
(1)主成分分析法。主成分分析是多元统计分析的一个分支。是将其分量相关的原随机向量,借助于一个正交变换,转化成其分量不相关的新随机向量,并以方差作为信息量的测度,对新随机向量进行降维处理。再通过构造适当的价值函数,进一步做系统转化。
(2)数据包络分析法。它是创建人以其名字命名的DEA模型——C2R模型。DEA法不仅可对同一类型各决策单元的相对有效性做出评价与排序,而且还可进一步分析各决策单元非DE有效的原因及其改进方向,从而为决策者提供重要的管理决策信息。
(3)模糊评价法。模糊评价法奠基于模糊数学。它不仅可对评价对象按综合分值的大小进行评价和排序,而且还可根据模糊评价集上的值按最大隶属度原则去评定对象的等级。
综合评价法的特点
综合评价法的特点表现为:
(1)评价过程不是逐个指标顺次完成的,而是通过一些特殊方法将多个指标的评价同时完成的;
(2)在综合评价过程中,一般要根据指标的重要性进行加权处理;
(3)评价结果不再是具有具体含义的统计指标,而是以指数或分值表示参评单位"综合状况"的排序。
综合评价法的要素
构成综合评价的要素主要有:
1.评价者。评价者可以是某个人或某团体。评价目的的给定、评价指标的建立、评价模型的选择、权重系数的确定都与评价者有关。因此,评价者在评价过程的作用是不可轻视的。
2.被评价对象。随着综合评价技术理论的开展与实践活动,评价的领域也从最初的各行各业经济统计综合评价拓展到后来的技术水平、生活质量、小康水平、社会发展、环境质量、竞争能力、综合国力、绩效考评等方面。这些都能构成被评价对象。
3.评价指标。评价指标体系是从多个视角和层次反映特定评价客体数量规模与数量水平的。它是一个“具体一抽象一具体”的辩证逻辑思维过程,是人们对现象总体数量特征的认识逐步深化、求精、完善、系统化的过程。
4.权重系数。相对于某种评价目的来说,评价指标相对重要性是不同的。权重系数确定的合理与否,关系到综合评价结果的可信程度。
5.综合评价模型。所谓多指标综合评价,就是指通过一定的数学模型将多个评价指标值“合成”为一个整体性的综合评价值。
综合评价法的步骤
1、确定综合评价指标体系,这是综合评价的基础和依据。
2、收集数据,并对不同计量单位的指标数据进行同度量处理。
3、确定指标体系中各指标的权数,以保证评价的科学性。
4、对经过处理后的指标在进行汇总计算出综合评价指数或综合评价分值。
5、根据评价指数或分值对参评单位进行排序,并由此得出结论。
综合评价分析指标值的计算方法
主要有打分综合法、打分排队法、综合指数法、功效系数法等。
17、什么是泊松分布
泊松分布(Poisson distribution),台译卜瓦松分布,是一种统计与概率学里常见到的离散机率分布(discrete probability distribution),由法国数学家西莫恩·德尼·泊松(Siméon-Denis Poisson)在1838年时发表。 泊松分布的概率密度函数为: P(X=k)=\frac{e^{-\lambda}\lambda^k}{k!} 泊松分布的参数λ是单位时间(或单位面积)内随机事件的平均发生率。 泊松分布适合于描述单位时间内随机事件发生的次数。如某一服务设施在一定时间内到达的人数,电话交换机接到呼叫的次数,汽车站台的候客人数,机器出现的故障数,自然灾害发生的次数等等。
(Poisson distribution),-{zh-cn:台译卜瓦松分布;zh-tw:也译为布瓦松分布,布阿松分布,波以松分布等}-,是一种统计与概率学里常见到的离散机率分布(discrete probability distribution),由法国数学家(Siméon-Denis Poisson)在1838年时发表。
泊松分布的概率密度函数为:
P(X=k)=\frac{e^{-\lambda}\lambda^k}{k!}
泊松分布的参数λ是单位时间(或单位面积)内随机事件的平均发生率。
18、什么是统计推断
统计在研究现象的总体数量关系时,需要了解的总体对象的范围往往是很大的,有时甚至是无限的,而由于经费、时间和精力等各种原因,以致有时在客观上只能从中观察部分单位或有限单位进行计算和分析,根据局部观察结果来推断总体。例如,要说明一批灯泡的平均使用寿命,只能从该批灯泡中抽取一小部分进行检验,推断这一批灯泡的平均使用寿命,并给出这种推断的置信程度。这种在一定置信程度下,根据样本资料的特征,对总体的特征做出估计和预测的方法称为统计推断法。统计推断是现代统计学的基本方法,在统计研究中得到了极为广泛的应用,它既可以用于对总体参数的估计,也可以用作对总体某些分布特征的假设检验。
统计推断是在概率论的基础上依据样本的有关数据和信息,对未知总体的质量特性参数,做出合理的判断和估计。它的一般过程如图l所示。
统计推断有着广泛的用途,几乎遍及所有科学技术领域,在质量管理活动中应用尤其普遍。因此,讨论统计推断是一个十分有意义的课题。
19、什么是五数概括法
五数概括法即用下面的五个数来概括数据:
最小值;
第1四分位数(Q1);
中位数(Q2);
第3四分位数(Q3);
最大值。
运用五数概括法的最简单的方式是首先将数据按递增顺序排列,然后很容易就能确定最小值、3个四分位数和最大值了。
五数概括法使用举例
对12个月薪数据的样本,按照递增顺序排列如下:
2210 2255 2350 | 2380 2380 2390 | 2420 2440 2450 | 2550 2630 2825
Q1=2365 Q2=2405 Q3=2500
(中位数)
中位数2405以及四分位数Q1=2365和Q3=2500前面已经计算出来了。对上述数据的观察可以知道最小值为2210,最大值为2825。因此,上述月薪数据以五数概括为:2210,2365,2405,2500,2825。在上述五数中相邻的每两个数之间,大约有1/4或25%的数据项。
20、什么是威尔科克森符号秩检验
威尔科克森符号秩检验是由威尔科克森(F·Wilcoxon)于1945年提出的。该方法是在成对观测数据的符号检验基础上发展起来的,比传统的单独用正负号的检验更加有效。它适用于T检验中的成对比较,但并不要求成对数据之差di服从正态分布,只要求对称分布即可。检验成对观测数据之差是否来自均值为0的总体(产生数据的总体是否具有相同的均值)。
威尔科克森符号秩检验的步骤
正负符号检验和威尔科克森符号秩检验,都可看作是就成对观察值而进行的参数方式的T检验的代用品,非参数检验具有无需对总体分布作假定的优点,而就成对观察值作的参数方式的T检验,必须假定有关的差别总体服从正态分布。
该方法具体步骤如下:
第一步:求出成对观测数据的差di,并将di的绝对值按大小顺序编上等级(曼-惠特尼U检验)。
第二步:等级编号完成以后恢复正负号,分别求出正等级之和T 和负等级之和T-,选择T 和T-中较小的一个作为威尔科克森检验统计量T。
第三步;作出判断。
根据显著性水平α查附表,得到临界值Tα,若T<Tα,则拒绝原假设H0。当观测值不少于20对时,统计量T的均值和方差分别为:
(近似服从标准正态分布)
若Z<-Zα(单侧)或Z<-Zα/2(双侧),则拒绝H0。
威尔科克森符号秩检验的应用举例
下面是分别用高锰酸钾法和EDTA法对某生长期蛋鸡配合料钙含量进行的7次测定结果(湖北省饲料质量监督检验站2002年常规检测样品),比较两种方法测定结果差异是否显著。
首先按大小顺序对两对观测值之差di进行等级排序,并加上正负号,分别计算正负等级之和:T =21,T-=-7。
高锰酸钾法和EDTA法测定蛋鸡配合料钙含量结果(%)
(注)编号4 和5 应该 为等级1和2,因为 di相同,所以(1 2)/2 ,分别为1.5. 编号1和7同理
假设两种方法检测饲料中钙含量结果无显著差异,即检验:
H0:两种方法检测结果无显著差异;
H1:两种方法检测结果有差异。
查附表得到,对于α=0.05的双侧检验,n=7 时,T0.025=2。由于 T =21> T0.025 ,则接受H0,可以认为两种方法测定饲料钙含量结果并无显著差异。
附表
威尔科克森带符号秩检验T的临界值表
21、什么是相关分析
相关分析就是对总体中确实具有联系的标志进行分析,其主体是对总体中具有因果关系标志的分析。它是描述客观事物相互间关系的密切程度并用适当的统计指标表示出来的过程。在一段时期内出生率随经济水平上升而上升,这说明两指标间是正相关关系;而在另一时期,随着经济水平进一步发展,出现出生率下降的现象,两指标间就是负相关关系。
为了确定相关变量之间的关系,首先应该收集一些数据,这些数据应该是成对的。例如,每人的身高和体重。然后在直角坐标系上描述这些点,这一组点集称为“散点图”。
根据散点图,当自变量取某一值时,因变量对应为一概率分布,如果对于所有的自变量取值的概率分布都相同,则说明因变量和自变量是没有相关关系的。反之,如果,自变量的取值不同,因变量的分布也不同,则说明两者是存在相关关系的。
两个变量之间的相关程度通过相关系数r来表示。相关系数r的值在-1和1之间,但可以是此范围内的任何值。正相关时,r值在0和1之间,散点图是斜向上的,这时一个变量增加,另一个变量也增加;负相关时,r值在-1和0之间,散点图是斜向下的,此时一个变量增加,另一个变量将减少。r的绝对值越接近1,两变量的关联程度越强,r的绝对值越接近0,两变量的关联程度越弱。
相关分析的种类
1、按相关的程度分为完全相关、不完全相关和不相关
1)两种依存关系的标志,其中一个标志的数量变化由另一个标志的数量变化所确定,则称完全相关,也称函数关系。
2)两个标志彼此互不影响,其数量变化各自独立,称为不相关。
3)两个现象之间的关系,介乎完全相关与不相关之间称不完全相关。
2、按相关的方向分为正相关和负相关
1)正相关指相关关系表现为因素标志和结果标志的数量变动方向一致。
2)负相关指相关关系表现为因素标志和结果标志的数量变动方向是相反的。
3、按相关的形式分为线性相关和非线性相关
一种现象的一个数值和另一现象相应的数值在指教坐标系中确定为一个点,称为线性相关。
4、按影响因素的多少分为单相关和复相关
1)如果研究的是一个结果标志同某一因素标志相关,就称单相关。
2)如果分析若干因素标志对结果标志的影响,称为复相关或多元相关。
相关分析的主要内容
1、确定相关关系的存在,相关关系呈现的形态和方向,相关关系的密切程度。其主要方法是绘制相关图表和计算相关系数。
1)相关表
编制相关表前首先要通过实际调查取得一系列成对的标志值资料作为相关分析的原始数据。
相关表的分类:简单相关表和分组相关表。
单变量分组相关表:自变量分组并计算次数,而对应的因变量不分组,只计算其平均值;该表特点:使冗长的资料简化,能够更清晰地反映出两变量之间相关关系。双变量分组相关表:自变量和因变量都进行分组而制成的相关表,这种表形似棋盘,故又称棋盘式相关表。
2)相关图
利用直角坐标系第一象限,把自变量置于横轴上,因变量置于纵轴上,而将两变量相对应的变量值用坐标点形式描绘出来,用以表明相关点分布状况的图形。相关图被形象地称为相关散点图。
因素标志分了组,结果标志表现为组平均数,所绘制的相关图就是一条折线,这种折线又叫相关曲线。
3)相关系数
相关系数是按积差方法计算,同样以两变量与各自平均值的离差为基础,通过两个离差相乘来反映两变量之间相关程度;着重研究线性的单相关系数。
2、确定相关关系的数学表达式。
3、确定因变量估计值误差的程度。
什么是移动平均法?
移动平均法是用一组最近的实际数据值来预测未来一期或几期内公司产品的需求量、公司产能等的一种常用方法。移动平均法适用于即期预测。当产品需求既不快速增长也不快速下降,且不存在季节性因素时,移动平均法能有效地消除预测中的随机波动,是非常有用的。移动平均法根据预测时使用的各元素的权重不同。
移动平均法是一种简单平滑预测技术,它的基本思想是:根据时间序列资料、逐项推移,依次计算包含一定项数的序时平均值,以反映长期趋势的方法。因此,当时间序列的数值由于受周期变动和随机波动的影响,起伏较大,不易显示出事件的发展趋势时,使用移动平均法可以消除这些因素的影响,显示出事件的发展方向与趋势(即趋势线),然后依趋势线分析预测序列的长期趋势。
移动平均法的种类
移动平均法可以分为:简单移动平均和加权移动平均。
一、简单移动平均法
简单移动平均的各元素的权重都相等。简单的移动平均的计算公式如下: Ft=(At-1 At-2 At-3 … At-n)/n式中,
Ft--对下一期的预测值;
n--移动平均的时期个数;
At-1--前期实际值;
At-2,At-3和At-n分别表示前两期、前三期直至前n期的实际值。
二、加权移动平均法
加权移动平均给固定跨越期限内的每个变量值以相等的权重。其原理是:历史各期产品需求的数据信息对预测未来期内的需求量的作用是不一样的。除了以n为周期的周期性变化外,远离目标期的变量值的影响力相对较低,故应给予较低的权重。 加权移动平均法的计算公式如下:
Ft=w1At-1 w2At-2 w3At-3 … wnAt-n式中,
w1--第t-1期实际销售额的权重;
w2--第t-2期实际销售额的权重;
wn--第t-n期实际销售额的权
n--预测的时期数;w1 w2 … wn=1
在运用加权平均法时,权重的选择是一个应该注意的问题。经验法和试算法是选择权重的最简单的方法。一般而言,最近期的数据最能预示未来的情况,因而权重应大些。例如,根据前一个月的利润和生产能力比起根据前几个月能更好的估测下个月的利润和生产能力。但是,如果数据时季节性的,则权重也应是季节性的。
移动平均法的优缺点
使用移动平均法进行预测能平滑掉需求的突然波动对预测结果的影响。但移动平均法运用时也存在着如下问题:
1、 加大移动平均法的期数(即加大n值)会使平滑波动效果更好,但会使预测值对数据实际变动更不敏感;
2、 移动平均值并不能总是很好地反映出趋势。由于是平均值,预测值总是停留在过去的水平上而无法预计会导致将来更高或更低的波动;
3、 移动平均法要由大量的过去数据的记录。
22、什么是物价指数
物价指数是反映计算期销售或购进的全部商品价格总水平比基期水平升降变动程度的相对数,通常以计算期(年度、季度或月度)与基期(某年度、季度或月度)相对比,以百分数表示。
物价指数是经济指数中比较复杂的一种相对数。按包括商品种类不同,分为单项商品价格指数、商品类别指数和总指数。按采用基期的不同,分为环比物价指数(以上一期为基期)、年距环比物价指数(以上年同期为基期)、定基物价指数(和固定时期比较)。按商品的种类和流通环节区分,有工业品出厂价格指数,农副产品收购价格指数、批发物价指数、零售物价指数、服务项目价格指数、职工生活费用价格指数、工农业商品的综合比价指数。按商品流通渠道区分,又可分为国营、集市贸易等物价指数。
计算物价指数除了要选择好基期和计算期外,还要选择好提供价格资料的典型地区,因为无法编制所有商品、所有市县的物价指数;要注意商品的可比性;要注意商品的代表性;要注意商品规格、等级、质量的一致性;要注意计算方法的科学性。
CPI的计算公式是 CPI=(一组固定商品按当期价格计算的价值)除以(一组固定商品按基期期价格计算的价值)乘以100。
23、什么是移动平均趋势剔除法
移动平均趋势剔除法,就是在现象具有明显长期趋势的情况下,测定季节变动的一种基本方法。
基本思路:先从时间数列中将长期趋势剔除掉,然后再应用“同期平均法”剔除循环变动和不规则变动,最后通过计算季节比率来测定季节变动的程度。
剔除长期趋势的方法一般用移动平均法。因此,它是长期趋势的测定方法——“移动平均法”和季节变动的测定方法——“同期平均法”的结合运用,在方法上没有新的思想。
移动平均趋势剔除法的步骤
“移动平均趋势剔除法”来测定季节变动趋势。其基本步骤如下:
第一,先根据各年的季度(或月度)资料(Y)计算四季(或12个月)的移动平均数,然后为了“正位”,再计算二季(月)移动平均数,作为各期的长期趋势值(T)。
第二,将实际数值(Y)除以相应的移动平均数(T),得到各期的Y/T。这就是消除了长期趋势影响的时间数列,它是一个相对数,称为季节指数。其结果为表中第四列数值。
第三,将Y/T重新按“同期平均法”计算季节比率的方式排列。然后,按照该方法要求,先计算“异年同季平均数”,然后再计算“异年同季平均数的平均数”,即消除长期趋势变动后,新数列的序时平均数;最后,计算季节比率并画图显示。
[例]根据表1的资料,按移动平均趋势剔除法计算销售量的季节指数。
解:首先求出12个月移动平均趋势值T,并求得Y/T,计算结果如表1。
表1 销售量季节指数计算表(Ⅰ) 单位:万件
然后将表1中的Y/T重新排列,如表2,求出各年同月平均数,使不规则变动消除,已是季节指数,但由于12个月的总和不等于1200%,需进行调整。其调整系数为:调整系数=
=0.009892,用调整系数乘以同月平均数,即得季节指数,见表2的最后一栏。
表2 销售量季节指数计算表(Ⅱ)
24、什么是卡方分布
若n个相互独立的随机变量ξ1,ξ2,…,ξn ,均服从标准正态分布(也称独立同分布于标准正态分布),则这n个服从标准正态分布的随机变量的平方和∑ξ2i构成一新的随机变量,其分布规律称为χ2(n)分布,其中参数 n 称为自由度,自由度不同就是另一个χ2分布,正如正态分布中均值或方差不同就是另一个正态分布一样。卡方分布是由正态分布构造而成的一个新的分布,这也正反映了前面所说的正态分布的重要性。
25、什么是预计估算法
预计估算法是根据现象在一段时间内已实现指标,分析后一段时间发展变化情况,估算即将实现指标的方法。这种方法,不仅需要掌握确凿的实际统计资料作为估算的依据,而且要求深入实际做好预计分析。
预计估算法的原则
为保证估算的准确性,应用预计估算法应遵循两个基本原则:
1、要根据长时间的实际统计信息估算短时间的统计数字。
例如,对年度预计估算,要根据前三个季度的实际统计信息估算第四季度的统计数字,而不能根据第一季度的实际统计信息估算后三个季度的统计数字。同样,对月度预计估算,要根据上、中旬的实际统计信息估算下旬的统计数字,而不能根据上旬的实际统计信息估算中、下旬的统计数字。原因在于短时间的根据不充分,很难把长时间的变化都估计在内,其结果是不可靠的。
2、要开展调查研究进行细致的预计分析。
预计估算不是数列曲线的简单引申,而是从实际出发的分析研究工作。例如,对年度生产计划完成情况的预计估算,不仅需要掌握前三个季度完成产量的实际统计信息,还要分析这三个季度生产发展速度和计划完成情况,后一个季度的季节变动因素,了解去年同期生产完成情况的实际统计信息,研究现在生产面临的矛盾和采取解决的积极措施。这样才能比较准确地估算出来生产计划预计完成程度。
设:某工业企业今年总产值计划比去年增长5%。前三个季度实际完成情况与去年同期相比增长8%;分析第四季度生产的有利措施和职工的积极性,预计与去年同期相比增长12%。去年总产值的30%是靠第四季度完成的。
要求:估算今年总产值计划完成情况。
年总产值预计增长%=frac{108%\times70% 112%\times30%}{100%}-100%= 9.2%
年总产值计划预计完成%=frac{109.2%}{105%}\times100%=104%
预计估算的重要作用在于提高统计研究工作的预见性。在事情发生之前,预先进行分析研究,估算可能达到的结果,以利于保证完成和超额完成计划。
26、什么是伽马分布
伽玛分布(Gamma distribution)是统计学的一种连续概率函数。
Gamma分布中的参数α,称为形状参数(shape parameter),β称为尺度参数(scale parameter)。
27、什么是统计检验
建立假设
统计检验是将抽样结果和抽样分布相对照而作出判断的工作。取得抽样结果,依据描述性统计的方法就足够了。抽样分布则不然,它无法从资料中得到,非利用概率论不可。而不对待概括的总体和使用的抽样程序做某种必要的假设,这项工作将无法进行。
求抽样分布
在做了必要的假设之后,我们就能用数学推理过程来求抽样分布了。由于数学上已经取得的成果,实际上统计工作者要做的这项工作往往并不是真的去求抽样分布的数学形式,而是根据具体需要,确定特定问题的统计检验应该采用哪种分布的数学用表。
选择显著性水平和否定域
有了与问题相关的抽样分布,我们便可以把所有可能的结果分成两类:一类是不大可能的结果;另一类人们预料这些结果很可能发生。既然如此,如果我们在一次实际抽样中得到的结果恰好属于第一类,我们就有理由对概率分布的前提假设产生怀疑。在统计检验中,这些不大可能的结果称为否定域。如果这类结果真的发生了,我们将否定假设;反之就不否定假设。概率分布的具体形式是由假设决定的,假设肯定不止一个。在统计检验中,通常把被检验的那个假设称为零假设(或称原假设,用符号H0表示),并用它和其他备择假设(用符号H1表示)相对比。值得注意的是,假设只能被检验,从来不能加以证明。统计检验可以帮助我们否定一个假设,却不能帮助我们肯定一个假设。为了使检验更严格、更科学,还需要更多的东西。首先,我们必须确定冒犯第一类和第二类错误的风险的程度;其次,要确定否定域是否要包含抽样分布的两端。第一类错误是,零假设H0实际上是正确的,却被否定了。第二类错误则是,H0实际上是错的,却没有被否定。第二类错误是,零假设H0实际上是错误的,却没有被否定。遗憾的是,不管我们如何选择否定域,都不可能完全避免第一类错误和第二类错误,也不可能同时把犯两类错误的危险压缩到最小。对任何一个给定的检验而言,第一类错误的危险越小,第二类错误的概率就越大;反之亦然。一般来讲,不可能具体估计出第二类错误的概率值。第一类错误则不然,犯第一类错误的概率是否定域内各种结果的概率之和。由于犯第一类错误的危险和犯第二类错误的危险呈相背趋向,所以统计检验时,我们必须事先在冒多大第一类错误的风险和多大第二类错误的风险之间作出权衡。被我们事先选定的可以犯第一类错误的概率,叫做检验的显著性水平(用α表示),它决定了否定域的大小。如果抽样分布是连续的,否定域可以建立在想要建立的任何水平上,否定域的大小可以和显著性水平的要求一致起来(后面的正态检验就如此)。如果抽样分布是非连续的,就要用累计概率的方法找出一组构成否定域的结果。即在已知概率分布表上,从两端可能性最小的概率开始向中心累计,直至概率之和略小于选定的显著性水平为止。在许多场合,我们能预测偏差的方向,或只对一个方向的偏差感兴趣。每当方向能被预测的时候,在同样显著性水平的条件下,单侧检验比双侧检验更合适。因为否定域被集中到抽样分布更合适的一侧,可以得到一个比较大的尾端。这样做,可以在犯第一类错误的危险不变的情况下,减少了犯第二类错误的危险。
计算检验统计量
完成了上述工作之后,接下来就是做一次与理想试验尽量相同的实际抽样(比如实际做一次重复抛掷硬币的试验),并从获取的样本资料算出检验统计量。检验统计量是关于样本的一个综合指标,但与第九章参数估计中将要讨论的统计量有所不同,它不用作估测,而只用作检验。
判定
假设检验系指拒绝或保留零假设的判断,又称显著性检定。在选择否定域并计算检验统计量之后,完成最后一道手续,即根据试验或样本结果决定假设的取与舍。如果结果落在否定域内,将在已知犯第一类错误概率的条件下,否定零假设。反之,如果结果落在否定域外,则不否定零假设,与此同时,就有了犯第二类错误的危险。
28、什么是拉丁方设计?
拉丁方设计(Latin square design)使研究人员得以在统计上控制两个不相互作用的外部变量并且操纵自变量。每个外部变量或分区变量被划分为一个相等数目的区组或级别,自变量也同样被分为相同数目的级别。
拉丁方以表格的形式被概念化,其中行和列代表两个外部变量中的区组,然后将自变量的级别分配到表中各单元中。简单的说就是某一变量在其所处的任意行或任意列中,只出现一次。
具体的说拉丁方是一种为减少实验顺序对实验的影响,而采取的一种平衡试验顺序的技术。采用的是一种拉丁方格做辅助,拉丁方格就是由需要排序的几个变量构成的正方形矩阵。其具体的应用过程是这样的:
当处理数是偶数时,其顺序是这样确定的,横排:1,2,n,3,n-1,4,n-2……(n代表要排序的量的个数),随后的次序是在第一个次序的数目上加“1”,直到形成拉丁方。
假设处理数是6,则拉丁方如下:
A B F C E D
B C A D F E
C D B E A F
D E C F B A
E F D A C B
F A E B D C
当处理数是奇数时,(以5为例)
(1)先按偶数法则形成一个拉丁方:
A B E C D
B C A D E
C D B E A
D E C A B
E A D B C
(2)然后把上述模式简单反过来,即形成:
D C E B A
E D A C B
A E B D C
B A C E D
C B D A E
29、什么是矩法估计
对于随机变量来说,矩是其最广泛,最常用的数字特征,母体ξ的各阶矩一般与ξ的分布中所含的未知参数有关,有的甚至就等于未知参数。由辛钦大数定律知,简单随机子样的子样原点矩
依概率收敛到相应的母体原点矩Eξr,r = 1,2,Λ。这就启发我们想到用子样矩替换母体矩(今后称之为替换原则),进而找出未知参数的估计,基于这种思想求估计量的方法称为矩法。用矩法求得的估计称为矩法估计,简称矩估计。它是由英国统计学家皮尔逊Pearson于1894年提出的。
矩法估计的理论依据
由辛钦大数定律知:
即对
,有
或
矩法估计的具体步骤
设母体ξ的概率函数为f(x,θ1,Λ,θk),其中
是k个未知参数,ξ1,Λ,ξn是取自这一母体的一个子样。设ξ的k阶矩vk = Eξk存在,则vj,j < k都存在,并且是θ1,Λ,θk的函数vj(θ1,Λ,θk),又子样ξ1,Λ,θk的j阶矩为
。我们设
(1)
这样我们就得到含k个未知参数θ1,Λ,θk的k个方程,解由这k个方程联列所构成的方程组就可以得到theta1,Λ,θk的一组解:
(2)
用(2)中的解
来估计参数θi 就是矩法估计。
一般我们考察
的情形。
在数理统计学中,我们一般用
表示θ的估计量。
下面我们举一个与实际问题有关的多参数的矩法估计问题。
例:已知大学生英语四级考试成绩ξ~N(μ,σ2),均值μ,方差σ2均未知,ξ1,Λ,ξn为取自母体ξ的一个子样,(x1,Λ,xn)是子样的一组观测值,求μ与σ2的矩法估计。
解:注意到有两个未知参数,由矩法估计知需两个方程,按照(1)式得方程组
解这一方程组得μ与σ的矩法估计量
从而μ与σ2的矩法估计值分别为
。
分析:注意到我们这里求出μ与σ2的矩法估计并未用到母体ξ的分布。这样对μ,σ2作出了估计,也就对整个母体分布作出了推断,进而对大学生英语四级考试成绩ξ相关的其它数字特征如标准分、标准差、偏态系数等作出了估计。
矩法估计的优缺点
矩法估计原理简单、使用方便,使用时可以不知母体的分布,而且具有一定的优良性质(如矩估计
为Eξ的一致最小方差无偏估计),因此在实际问题,特别是在教育统计问题中被广泛使用。
但在寻找参数的矩法估计量时,对母体原点矩不存在的分布如柯西分布等不能用,另一方面它只涉及母体的一些数字特征,并未用到母体的分布,因此矩法估计量实际上只集中了母体的部分信息,这样它在体现母体分布特征上往往性质较差,只有在样本容量n较大时,才能保障它的优良性,因而理论上讲,矩法估计是以大样本为应用对象的。
30、什么是卡方检验
卡方检验是一种用途很广的计数资料的假设检验方法。它属于非参数检验的范畴,主要是比较两个及两个以上样本率( 构成比)以及两个分类变量的关联性分析。其根本思想就是在于比较理论频数和实际频数的吻合程度或拟合优度问题。
它在分类资料统计推断中的应用,包括:两个率或两个构成比比较的卡方检验;多个率或多个构成比比较的卡方检验以及分类资料的相关分析等。
卡方检验的基本思想
卡方检验是以χ2分布为基础的一种常用假设检验方法,它的无效假设H0是:观察频数与期望频数没有差别。
该检验的基本思想是:首先假设H0成立,基于此前提计算出χ2值,它表示观察值与理论值之间的偏离程度。根据χ2分布及自由度可以确定在H0假设成立的情况下获得当前统计量及更极端情况的概率P。如果P值很小,说明观察值与理论值偏离程度太大,应当拒绝无效假设,表示比较资料之间有显著差异;否则就不能拒绝无效假设,尚不能认为样本所代表的实际情况和理论假设有差别。
卡方值的计算与意义
χ2值表示观察值与理论值之问的偏离程度。计算这种偏离程度的基本思路如下。
(1)设A代表某个类别的观察频数,E代表基于H0计算出的期望频数,A与E之差称为残差。
(2)显然,残差可以表示某一个类别观察值和理论值的偏离程度,但如果将残差简单相加以表示各类别观察频数与期望频数的差别,则有一定的不足之处。因为残差有正有负,相加后会彼此抵消,总和仍然为0,为此可以将残差平方后求和。
(3)另一方面,残差大小是一个相对的概念,相对于期望频数为10时,期望频数为20的残差非常大,但相对于期望频数为1 000时20的残差就很小了。考虑到这一点,人们又将残差平方除以期望频数再求和,以估计观察频数与期望频数的差别。
进行上述操作之后,就得到了常用的χ2统计量,由于它最初是由英国统计学家Karl Pearson在1900年首次提出的,因此也称之为Pearson χ2,其计算公式为
其中,Ai为i水平的观察频数,Ei为i水平的期望频数,n为总频数,pi为i水平的期望频率。i水平的期望频数Ei等于总频数n×i水平的期望概率pi,k为单元格数。当n比较大时,χ2统计量近似服从k-1(计算Ei时用到的参数个数)个自由度的卡方分布。
作为学术界的领袖,Pearson先生当初发表在《哲学杂志》上的χ2论文题目为:On the criterion that a given system of deviations from the probable in the case of a correlated system of variables is such that it can be reasonably supposed to have arisen from random sampling.
由卡方的计算公式可知,当观察频数与期望频数完全一致时,χ2值为0;观察频数与期望频数越接近,两者之间的差异越小,χ2值越小;反之,观察频数与期望频数差别越大,两者之间的差异越大,χ2值越大。换言之,大的χ2值表明观察频数远离期望频数,即表明远离假设。小的χ2值表明观察频数接近期望频数,接近假设。因此,χ2是观察频数与期望频数之间距离的一种度量指标,也是假设成立与否的度量指标。如果χ2值“小”,研究者就倾向于不拒绝H0;如果χ2值大,就倾向于拒绝H0。至于χ2在每个具体研究中究竟要大到什么程度才能拒绝H0,则要借助于卡方分布求出所对应的P值来确定。
卡方检验的样本量要求
卡方分布本身是连续型分布,但是在分类资料的统计分析中,显然频数只能以整数形式出现,因此计算出的统计量是非连续的。只有当样本量比较充足时,才可以忽略两者问的差异,否则将可能导致较大的偏差具体而言,一般认为对于卡方检验中的每一个单元格,要求其最小期望频数均大于1,且至少有4/5的单元格期望频数大于5,此时使用卡方分布计算出的概率值才是准确的。如果数据不符合要求,可以采用确切概率法进行概率的计算。
卡方检验的类型
1、四格表资料的卡方检验
四格表资料的卡方检验用于进行两个率或两个构成比的比较。
1)专用公式:
若四格表资料四个格子的频数分别为a,b,c,d,则四格表资料卡方检验的卡方值=
,自由度v=(行数-1)(列数-1)
2)应用条件:
要求样本含量应大于40且每个格子中的理论频数不应小于5。当样本含量大于40但理论频数有小于5的情况时卡方值需要校正,当样本含量小于40时只能用确切概率法计算概率。
2、行×列表资料的卡方检验
行×列表资料的卡方检验用于多个率或多个构成比的比较。
1)专用公式:
r行c列表资料卡方检验的卡方值=
2)应用条件:
要求每个格子中的理论频数T均大于5或1<T<5的格子数不超过总格子数的1/5。当有T<1或1<T<5的格子较多时,可采用并行并列、删行删列、增大样本含量的办法使其符合行×列表资料卡方检验的应用条件。而多个率的两两比较可采用行×列表分割的办法。
3、列联表资料的卡方检验
同一组对象,观察每一个个体对两种分类方法的表现,结果构成双向交叉排列的统计表就是列联表。
1)R×C 列联表的卡方检验:
R×C 列联表的卡方检验用于R×C列联表的相关分析,卡方值的计算和检验过程与行×列表资料的卡方检验相同。
2)2×2列联表的卡方检验:
2×2列联表的卡方检验又称配对记数资料或配对四格表资料的卡方检验,根据卡方值计算公式的不同,可以达到不同的目的。当用一般四格表的卡方检验计算时,卡方值=(ad-bc)2n/(a b)(c d)(a c)(b d),此时用于进行配对四格表的相关分析,如考察两种检验方法的结果有无关系;当卡方值=( | b − c | − 1)2/(b c)时,此时卡方检验用来进行四格表的差异检验,如考察两种检验方法的检出率有无差别。
列联表卡方检验应用中的注意事项同R×C表的卡方检验相同。
卡方检验的用途
卡方检验最常见的用途就是考察某无序分类变量各水平在两组或多组间的分布是否一致实际上,除了这个用途之外.膏方检验还有更广泛的应用。具体而言,其用途主要包括以下几个方面:
(1)检验某个连续变量的分布是否与某种理论分布相一致。如是否符合正态分布、是否服从均匀分布、是否服从Poisson分布等。
(2)检验某个分类变量各类的出现概率是否等于指定概率。如在36选7的抽奖中,每个数字出现的概率是否各为1/36;掷硬币时,正反两面出现的概率是否均为0.5。
(3)检验某两个分类变量是否相互独立。如吸烟(二分类变量:是、否)是否与呼吸道疾病(二分类变量:是、否)有关;产品原料种类(多分类变量)是否与产品合格(二分类变量)有关。
(4)检验控制某种或某几种分类因素的作用以后,另两个分类变量是否相互独立。如在上例中,控制性别、年龄因素影响以后,吸烟是否和呼吸道疾病有关;控制产品加工工艺的影响后,产品原料类别是否与产品合格有关。
(5)检验某两种方法的结果是否一致。如采用两种诊断方法对同一批人进行诊断,其诊断结果是否一致;采用两种方法对客户进行价值类别预测,预测结果是否一致。
卡方检验的应用条件
适用于四格表应用条件:
1)随机样本数据。两个独立样本比较可以分以下3种情况:
(1)所有的理论数T≥5并且总样本量n≥40,用Pearson卡方进行检验。
(2)如果理论数T<5但T≥1,并且1≥40,用连续性校正的卡方进行检验。
(3)如果有理论数T<1或n<40,则用Fisher’s检验。
2)卡方检验的理论频数不能太小。
R×C表卡方检验应用条件:
(1)R×C表中理论数小于5的格子不能超过1/5;
(2)不能有小于1的理论数。如果实验中有不符合R×C表的卡方检验,可以通过增加样本数、列合并来实现。
31、什么是模糊统计分组法
随着社会科技的不断发展,统计学科在各门学科的地位越来越高,但传统的统计分组方法却因统计对象的日趋复杂而逐渐失去其可靠性,因此,必须引入新的统计分组方法。
由于统计对象带有许多不确定性,即模期性因素,使统计分组法随着统计对象的日趋复杂而逐渐失去其可靠性。我们在该文中建立r模糊统计分组的数学模型,并应用该模型,给出了五个大中型企业生产规模的模期统计分组算法,此方法的结果大大提高r统计分组的可靠性
一、传统的统计分组法及问题
根据现象总体内在特点和统计工作任务的要求,按照某一个或几个标志,把总体分为不同类型或者性质不同的几个部分,称为统计分组。统计分组是统计分析的主要方法,它对引导国民经济的正常发展起着重大的作用。
正确选择分组标志是科学分组的关键。分组标志选择得当与否直接影响分组的作用和效果,由于分类方法的不同,同一材料却得出完全相反的结论。
例如,反映工业企业规模的标志有职工人数、固定资产价值、总价值等。不同工业部门选择企业规模的标志可以不同。劳动密集型行业可按职工人数分组;技术密集型企业采用固定资产价值的标志就可能更好些。可见,必须根据具体情况来确定。但传统的统计分组法叉存在以下三方面的问题。
(1)往往只选择一个标志,而忽视r其他标志的作用。如在确定企业的规模时,对劳动密集型企业按职工人数分组,忽视了技术、设备等方面的作用。
(2)主标志确定后,其本身内部的差别也完全被忽视。如上例中,按职工人数分组时,职工素质的差异就没有反映出来。
(3)分组结果太粗略,例如,确定企业的规模时就简单用大、中、小型企业来划分。
从以上分析可看出,统计分组本身所存在的缺陷将随着社会的发展越来越明显。事实上,对社会企业这样大的系统,要用模糊数学方法才能得到较精确的描述。本文提出的模糊统计分组法就基本上克服了上述三方面问题。
二、模糊统计分组法
对总体进行划分时,各个标志都将起作用,而且每个标志本身的差异也应该适当加以考虑。下面利用综合评判模型来建立模糊统计分组的数学模型,井就如何确定企业的生产规模来展开讨论。
1、数学模型
设有二元有限论域
其中X代表统计研究的对象集。例如,代表n个企业等,而Y代表统计标志集,把模糊变换。
A * R = B
称为模糊统计分组法的数学模型。这里R是X×Y上的一个模糊关系,即是一个m×n模糊短阵,A是论域Y上的模糊子集,即各标志的权重,而B是统计分组的结果,它是论域X上的一个模糊子集,即模糊向量。
出于标志本身内部存在差异,如对企业规模来说,在职工人数这个标志中就有普通工人、技术员、工程师的差剐,因此应考虑多层次综合评判,我们考虑二级模型。
(1)对标志集
中每一个标志
,它可以有Ki个评判指标。
首先对它进行综合评判折算。
(2)应用模糊统计分组模型进行评刿。
2、具体算例
下面我们用几个企业的统计资料(见表1)来建立数学模型,这里用二级模型。
(1)首先进行每个标志的评判折算。
① 对职工人数进行评判。假设每个工人都具有平均劳动熟练程度和强度,一个技术员相当于3个工人,一个工程师相当于lO个工人,一个高级工程师相当于l5个工人。这里有较大的主观因素,对具体情况可分别确定,因为随着时代的发展,现代技术人才的作用越来越大。
②对固定资产价值进行评判。这里主要是旧设备的折旧问题,应当指出:购置的设备即使从未使用过,也会受时间的磨损(包括产品更新等)。主要是技术进步,成本降底产生的影响。饲如,计算机等高技术产品价格下降特别快,其本身就比较复杂,需要分类进行处理,转化成新价值进行计算。最后得到各企业职工人数及新价值折合数如表2。
(2)进行综合评判,分以下三步。
①特征值的规格化处理。规格化处理的方法较多,在这里我们选用比较合理的与最大值的比值法。因为根据上述的作法,可知企业规模与职工人数成正比,与新价值成正比。假定所有要考虑的企业中职工人数最多的是1O万人,新价值为一亿元。则可得到规格化模糊矩阵。
②决定权重。确定企业当时的生产规模时,假定当时工人的权重系数为0.3,新价值为0.7,则A=(O.3,0.7)。
③在确定企业生产规模时,每一标志都将起作用、因此采用有界和(θ)与普通实数乘法(·)算子:
向量B中的0.56525是四川蛇纹石厂的隶属度,0.4005是四川新康石棉厂的隶属度,0.38722是四川云阳糖厂的隶属度,0.51656是新庄发电厂 的隶属度。由此可见,四个企业中的四川蛇纹石厂的规模最大,而四川云阳糖厂的规模最小。
三、结论
这里所提出的模糊统计分组法解决了传统统计分组法中不可避免的三个问题,而且从具体算例中可以看出它具有以下几点好处。
(1)不同类型的企业也可以放在一起进行比较。
(2)克服了由于标志的选择不同得出不同结论的矛盾。
(3)可以及时发现企业存在的问题。例如,通过比较发现四川新康石棉厂技术力量最雄厚,人也最多,但设备陈旧,因此生产规模不大,说明这是一个埋没人才的地方,同时,也说明国家人才流动政策的重要性。
(4)企业人才与设备应该合理配置。
32、什么是平衡估算法
平衡估算法是根据客观现象之间的平衡关系来推算某项统计指标的方法。客观现象之间的互相联系,不仅可以表现为一种因素关系,而且可以表现为一种平衡关系。
平衡估算法举例
例如,居民货币收支结存之间就存在着平衡关系,即:
年初货币结存+本年货币收入+本年货币流入=本年货币支出+本年货币流出+年末货币结存
其中:居民本年货币支出包括两部分,一部分购买消费品支出,即居民商品购买力;另一部分购买文化生活服务及其他支出。我们利用居民货币收支的平衡关系,可以估算居民商品购买力。
设:某地区居民年初货币结存120万元,本年货币收入25000万元,本年货币流入730万元,本年用于购买文化生活服务等各项支出7000万元,本年货币流出600万元,年末货币结存150万元。
要求:应用平衡估算法推算本年居民商品购买力。
解:本年居民商品购买力=年初货币结存 本年货币收入 本年货币流入-本年购买文化生活服务等支出-本年货币流出-年末货币结存=120+25000+730-7000-600-150=18100(万元)
应用平衡估算法时要注意:平衡关系中的收支项目不能存在重复或遗漏现象,计算口径要一致,否则,估算结果会引起误差。同时,在这些收支平衡项目中,有的项目本身就要经过比较复杂的估算。例如,年初或年末的货币结存中,居民手里存放的现金数量;地区间货币的时而带出时而带入的数量;等等,估算难度都较大。这就要求收支平衡项目的计算必须符合实际情况,以保证推算指标的准确性。
33、什么是斯皮尔曼等级相关
斯皮尔曼等级相关是根据等级资料研究两个变量间相关关系的方法。它是依据两列成对等级的各对等级数之差来进行计算的,所以又称为“等级差数法”。
斯皮尔曼等级相关对数据条件的要求没有积差相关系数严格,只要两个变量的观测值是成对的等级评定资料,或者是由连续变量观测资料转化得到的等级资料,不论两个变量的总体分布形态、样本容量的大小如何,都可以用斯皮尔曼等级相关来进行研究。
斯皮尔曼等级相关系数
斯皮尔曼等级相关系数是反映两组变量之间联系的密切程度,它和相关系数r一样,取值在-1到 1之间,所不同的是它是建立在等级的基础上计算的。
现结合一个例子来加以说明,某工厂对工人的业务进行了一次考试,欲研究考试成绩与每月产量之间是否有联系,若随机抽选了一个样本,其考试成绩和产量数字如下表:
从表中的数字可以看出,工人的考试成绩愈高其产量也愈高,二者之间的联系程度是很一致的,但是相关系数r=0.676 并不算太高,这是由于它们之间的关系并不是线性的,如果分别按考试成绩和产量高低变换成等级(见上表第3、4列),则可以计算它们之间的等级相关系数为1。计算等级相关系数可以将数据变换成等级以后用原有的相关系数公式计算,也可以将算出每一对样本的等级之差di,然后用下列公式计算:
在所举的例子中由于等级完全一致,所有的di = 0,所以r=1。等级相关系数和通常的相关系数一样,它与样本的容量有关,尤其是在样本容量比较小的情况下,其变异程度较大,等级相关系数的显著性检验与普通的相关系数的显著性检验相同。
34、什么是T检验
T检验,亦称student t检验(Student's t test),主要用于样本含量较小(例如n<30),总体标准差σ未知的正态分布资料。
T检验是用于小样本(样本容量小于30)的两个平均值差异程度的检验方法。它是用T分布理论来推断差异发生的概率,从而判定两个平均数的差异是否显著。
T检验是戈斯特为了观测酿酒质量而发明的。戈斯特在位于都柏林的健力士酿酒厂担任统计学家。戈斯特于1908年在Biometrika上公布T检验,但因其老板认为其为商业机密而被迫使用笔名(学生)。
T检验的适用条件:正态分布资料
单个样本的t检验
目的:比较样本均数 所代表的未知总体均数μ和已知总体均数μ0。
计算公式:
t统计量:
自由度:v=n - 1
适用条件:
(1) 已知一个总体均数;
(2) 可得到一个样本均数及该样本标准误;
(3) 样本来自正态或近似正态总体。
单个样本的t检验实例分析
例1 难产儿出生体重
一般婴儿出生体重μ0 = 3.30(大规模调查获得),问相同否?
解:1.建立假设、确定检验水准α
H0:μ = μ0 (难产儿与一般婴儿出生体重的总均数相等;H0无效假设,null hypothesis)
(难产儿与一般婴儿出生体重的总均数不等;H1备择假设,alternative hypothesis,)
双侧检验,检验水准:α = 0.05
2.计算检验统计量
3.查相应界值表,确定P值,下结论
查附表1: t0.05 / 2.34 = 2.032,t = 1.77,t < t0.05 / 2.34,P > 0.05,按α = 0.05水准,不拒绝H0,两者的差别无统计学意义,尚不能认为难产儿平均出生体重与一般婴儿的出生体重不同
配对样本t检验
配对设计:将受试对象的某些重要特征按相近的原则配成对子,目的是消除混杂因素的影响,一对观察对象之间除了处理因素/研究因素之外,其它因素基本齐同,每对中的两个个体随机给予两种处理。
两种同质对象分别接受两种不同的处理,如性别、年龄、体重、病情程度相同配成对。
同一受试对象或同一样本的两个部分,分别接受两种不同的处理
自身对比。即同一受试对象处理前后的结果进行比较。
目的:判断不同的处理是否有差别
计算公式及意义:
t 统计量:
自由度:v=对子数-1
适用条件:配对资料
T检验的步骤
1、建立虚无假设H0:μ1 = μ2,即先假定两个总体平均数之间没有显著差异;
2、计算统计量t值,对于不同类型的问题选用不同的统计量计算方法;
1)如果要评断一个总体中的小样本平均数与总体平均值之间的差异程度,其统计量t值的计算公式为:
2)如果要评断两组样本平均数之间的差异程度,其统计量t值的计算公式为:
3、根据自由度df=n-1,查t值表,找出规定的t理论值并进行比较。理论值差异的显著水平为0.01级或0.05级。不同自由度的显著水平理论值记为t(df)0.01和t(df)0.05
4、比较计算得到的t值和理论t值,推断发生的概率,依据下表给出的t值与差异显著性关系表作出判断。
5、根据是以上分析,结合具体情况,作出结论。
T检验举例说明
例如,T检验可用于比较药物治疗组与安慰剂治疗组病人的测量差别。理论上,即使样本量很小时,也可以进行T检验。(如样本量为10,一些学者声称甚至更小的样本也行),只要每组中变量呈正态分布,两组方差不会明显不同。如上所述,可以通过观察数据的分布或进行正态性检验估计数据的正态假设。方差齐性的假设可进行F检验,或进行更有效的Levene's检验。如果不满足这些条件,只好使用非参数检验代替T检验进行两组间均值的比较。
T检验中的P值是接受两均值存在差异这个假设可能犯错的概率。在统计学上,当两组观察对象总体中的确不存在差别时,这个概率与我们拒绝了该假设有关。一些学者认为如果差异具有特定的方向性,我们只要考虑单侧概率分布,将所得到t-检验的P值分为两半。另一些学者则认为无论何种情况下都要报告标准的双侧T检验概率。
1、数据的排列
为了进行独立样本T检验,需要一个自(分组)变量(如性别:男女)与一个因变量(如测量值)。根据自变量的特定值,比较各组中因变量的均值。用T检验比较下列男、女儿童身高的均值。
2、T检验图
在T检验中用箱式图可以直观地看出均值与方差的比较,见下图:
这些图示能够很快地估计并且直观地表现出分组变量与因变量关联的强度。
3、多组间的比较
科研实践中,经常需要进行两组以上比较,或含有多个自变量并控制各个自变量单独效应后的各组间的比较,(如性别、药物类型与剂量),此时,需要用方差分析进行数据分析,方差分析被认为是T检验的推广。在较为复杂的设计时,方差分析具有许多t-检验所不具备的优点。(进行多次的T检验进行比较设计中不同格子均值时)。
T检验注意事项
要有严密的抽样设计随机、均衡、可比
选用的检验方法必须符合其适用条件(注意:t检验的前提是资料服从正态分布)
单侧检验和双侧检验
单侧检验的界值小于双侧检验的界值,因此更容易拒绝,犯第Ⅰ错误的可能性大。
假设检验的结论不能绝对化
不能拒绝H0,有可能是样本数量不够拒绝H0 ,有可能犯第Ⅰ类错误
正确理解P值与差别有无统计学意义
P越小,不是说明实际差别越大,而是说越有理由拒绝H0 ,越有理由说明两者有差异,差别有无统计学意义和有无专业上的实际意义并不完全相同
假设检验和可信区间的关系
结论具有一致性
差异:提供的信息不同
区间估计给出总体均值可能取值范围,但不给出确切的概率值,假设检验可以给出H0成立与否的概率
单个来源中国统计网,感谢原作者。 数据小编汇总整理。\(^o^)/~
,