
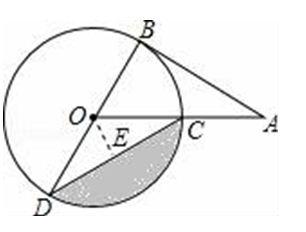
【考点】切线的性质;扇形面积的计算.
【分析】过O点作OE⊥CD于E,首先根据切线的性质和直角三角形的性质可得∠AOB=60°,再根据平角的定义和三角形外角的性质可得∠COD=120°,∠OCD=∠ODC=30°,根据含30°的直角三角形的性质可得OE,CD的长,再根据阴影部分的面积=扇形OCD的面积﹣三角形OCD的面积,列式计算即可求解

更多精选经典题型实时更新,你不容错过! 敬请点击 关注:第二学习课堂 查看更新和与老师实时互动。
,


【考点】切线的性质;扇形面积的计算.
【分析】过O点作OE⊥CD于E,首先根据切线的性质和直角三角形的性质可得∠AOB=60°,再根据平角的定义和三角形外角的性质可得∠COD=120°,∠OCD=∠ODC=30°,根据含30°的直角三角形的性质可得OE,CD的长,再根据阴影部分的面积=扇形OCD的面积﹣三角形OCD的面积,列式计算即可求解

更多精选经典题型实时更新,你不容错过! 敬请点击 关注:第二学习课堂 查看更新和与老师实时互动。
,