写在前面的话:码字不易,点个赞关注一下作者再走吧[呲牙]
================================
1. Wilcoxon检验Wilcoxon检验包含 2 种不同类型的检测,并且极容易混淆,这 2 种分别方法是
Wilcoxon rank-sum test:秩和检验,也称为Mann-Whitney U检验
Wilcoxon signed-rank test:符号秩检验
2.1秩和检验属于非参数检验,用于检验两个“独立样本”是否来自同一分布,不要求被检验的 2 组数据包含相同个数的元素,换句话说,秩和检验更适用于“非成对数据”之间的差异性检测。常见的情形有:
比较pre-AML组和正常control组之间VAF的大小分布
A组有15个人,B组有10个人,比较A组和B组的身高
……
秩和检验用于推断计量资料或等级资料的两个独立样本所来自的两个总体分布位置是否有差别。这是一种非参数替代配对双样本t检验,其可以被用于比较样品的两个独立的组。当数据不是正态分布且经过一定的数值转换尝试后,仍然无法满足正态性要求时使用,它将两独立样本组的非正态样本值进行比较。
2.2计算原理Wilcoxon秩和检验是基于样本数据秩和。
先将两样本看成是单一样本(混合样本),然后由小到大排列观察值统一编秩。
如果原假设两个独立样本来自相同的总体为真:秩将大约均匀分布在两个样本中。小的、中等的、大的秩值应该大约均匀被分在两个样本中。
如果备选假设两个独立样本来自不相同的总体为真:其中一个样本将会有更多的小秩值,这样就会得到一个较小的秩和;另一个样本将会有更多的大秩值,因此就会得到一个较大的秩和。
2.3 计算实例假设有A组和B组患者生存时间的数据:

image.png
现在使用秩和检验判断这 2 组数据是否存在显著性差异。
解答过程:
1.建立假设:两组数据来自同一总体,之间没有差异。
2.将A和B组数据整合成一个序列,并按升序重新排序。分别计算2组数据的排名之和。注意,当我们计算若干等值元素的排名时,会用这些元素排名的平均值作为它们在整个序列中的排名。例如,A组中的第1个元素与B组中第5个元素的值都等于5,且这2个5在整个序列中的排名分别是第5和第6,因此这两个元素的排名为(5 6)/2=5.5。其余等值元素的排名计算也与之类似。
A组排名之和:
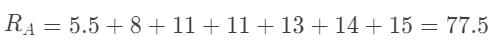
676be1bb930ef4b372249ee0284f098a.png
B组排名之和:

ff743f58efc0787d5add3090203909a5.png
3.令和分别表示A组和B组数据的个数,即

dfb82c1a793910593d1954a3e8b2c222.png
根据计算公式可得和的值:

98e8eb0a17eae84e8cef1c0b8e75399e.png

1dc16fe565b6df68ab5f682eed9fa7a5.png
4.因为 6.5<49.5,所以根据较小的 W值查表,得到 P=0.01393<0.05
2.4.Python实现Wilcoxon Rank Sum test可以看到结果是一致的
import scipy.stats as ss
# 两组列表数据
x=[5,6,7,7,8,9,10]
y=[3,4,4,4,5,6,6,7]
scipy.stats.ranksums(x, y)
RanksumsResult(statistic=2.4881415181387316, pvalue=0.012841262337219548)
用来检验“两独立配对样本”所来自的总体的分布是否存在显著差异的非参数方法。常见的情形有:同一受试对象的两个部分接受不同的处理(如对于一批血清样本,将其分为两个部分,利用不同的方法接受某种化合物的检验,检验结果的差异)
同一受试对象的自身前后对照(如检验癌症患者术前、术后的某种指标的差异)……
3.2 计算原理分别用第二组样本的各个观察值减去第一组对应样本的观察值。差值为正则记为正号,差值为负则记为负号。
将正号的个数与负号的个数进行比较,容易理解:如果正号个数和负号个数大致相当,则可以认为第二组样本大于第一组样本变量值的个数与第二组样本小于第一组样本的变量值个数是大致相当的,反之,差距越大。
3.3 计算实例研究先后出生的孪生兄弟间智力是否存在差异,对12对孪生兄弟的智力进行测试,结果见下表:

image.png
上述数据为12对孪生兄弟之间的智力得分,需要判断每对孪生兄弟之间的智力得分差异,测量指标为智力得分,属于配对设计的定量资料。对孪生兄弟之间的智力得分差值进行正态性检验,可以发现智力得分的差值不符合正态分布,因此本数据选用配对样本的秩和检验。
解答过程
1.建立假设:先后出生顺序对于智商没有影响。
2.对所有数据对两两求差,得到差异的正负符号以及差值的绝对值,并根据绝对值的大小进行排序。注意:当差值绝对值为0时,不计算该值的排名。3.计算大于0 和小于0 的秩和,并计算得到最终的统计值W值:
大于0的秩和:

3410ce286b65c49e003eaabe89c8922e.png
小于0的秩和:

b305b50cf5b4eea8e4cec1eb9ecc62c1.png
统计值W值:

c3449f5d69d89d79c0f1ba7901da0e06.png
4.所以根据W值查表,得到 P=0.4765<0.05
3.4.Python实现Wilcoxon signed-rank test可以看到结果是一致的!
from scipy import stats
before = [86,71,77,68,91,72,77,91,70,71,88,87]
after = [88,77,76,64,96,72,65,90,65,80,81,72]
#correction:如果为True,则是在小样本情况下,在计算Z统计量时用0.5来连续性校正。默认值为False。
#alternative:等于 “two-sided” 或 “greater” 或 “less”。“two-sided” 为双边检验,“greater” 为备择假设是大于的单边检验,“less” 为备择假设是小于的单边检验。
stats.wilcoxon(before,after,correction=True,alternative = 'two-sided')





