讲整体约分与连锁约分之前,
先回想一下,
分数的四则基本运算法则。
分数的加减运算:
同分母,分母不变,分子之间相加减;
异分母,分母先通分,分子再加减。
分数的乘除运算:
分子乘分子,分母乘分母;
除以一个分数,等于乘以它的倒数。
带分数需要先化为假分数,再进行乘除运算。
基础知识回顾完了,
一起来看看下面这道例题。
【例题1】计算

题目拿到手,
不要急着下笔,
分析完题目,
看看有没有规律,
再考虑动笔计算。
式子中,
第一个括号(被除数),分母分别为7和8,
第二个括号(除数),分母也分别为7和8。
两个括号内都是带分数。
分数的四则运算规则中,
带分数乘除运算前,需要先化为假分数。
我们把式子化成假分数看看,

这时候,我们发现:
第一个括号(被除数)两个分数的分子都是33,
第二个括号(除数)两个分数的分子都是11,
33刚好是11的倍数。
我们把第一个括号,提出来一个公因数3,

答案是不是一眼就看出来了?
等于3。
至于括号中的11/7,11/8的和就不需要再通分计算了,
我们把括号内直接看成整体,约分掉就行啦。

整体约分是分数计算中的一种简便方法,
可以帮助我们更快更好地算出答案。
总结一下整体约分的规律:
1、被除数和除数中分式的分母对应相同;
2、遇到带分数考虑化成假分数,遇到假分数呢?反过来,把它化成带分数就行了;
3、提取公因数,其余的整体约分。
再来看看,什么是连锁约分?
【例题2】计算

又是大分数的计算,
不要紧张哦,
遇到这种题目,往往都会有规律可循。
第一个括号内,1-1/1000=999/1000;
第二个括号内,1-1/999=998/999;
第三个括号内,1-1/998=997/998;
第四个括号内,1-1/997=996/997。
我们化简后看看得出什么?
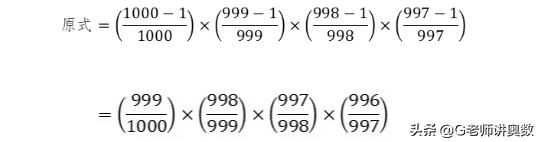
乘式中
第一项的分子999,
第二项的分母是999,
第二项的分子998,
第三项的分母是998,
第三项的分子997,
第四项的分母是997,
这些不是刚好可以约分掉吗?

最后剩下的结果就是:
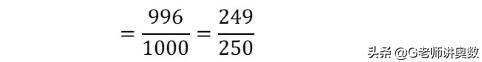
第一项的分母1000,
第四项的分子996,
其余的分子分母,分别约分掉了。
就像起了一个连锁反应,
所以,
这种约分方法就称之为“连锁约分”。
总结一下连锁约分的规律:
1、计算式中有多个分式相乘;
2、各个因式中的分子、分母分别化成乘积形式;
3、观察规律,约分,得出结果。