绝对值是初中代数中的一个基本概念,是学习相反数、有理数运算及后续算术根的基础。绝对值又是初中代数中的一个重要概念,在解代数式化简求值、解方程(组)、解不等式(组)等问题中有着广泛的应用,全面理解、掌握绝对值这一概念,应从以下方面入手:
1.去绝对值的符号法则:
①丨a丨=a(a>0);
②丨a丨=0(a=0);
③丨a丨=-a(a<0)。
2.绝对值的基本性质:
①非负性:丨a丨≥0;
②丨a丨丨b丨=丨a丨丨b丨;
③丨a/b丨=丨a丨/丨b丨(b≠0);
④丨a²丨=丨a²丨=a²;
⑤丨a d丨≤丨a丨 丨b丨;
⑥丨丨a丨-丨b丨丨≤丨a-b丨≤丨a丨 丨b丨;
3.绝对值的几何意义:
从数轴上看,丨a丨表示数a的点到原点的距离(长度,非负);丨a-b丨表示数a、数b两点间的距离。
例题1:
(1)已知丨×丨=5,丨y丨=1,那么丨丨x-y丨-丨x y丨丨=______。
(2)非零整数m,n满足丨m丨 丨n丨-5=0,所有这样的整数组(m,n)共有______组。
解题思路
(1)可以对x,y的取值进行分类求解,又可以利用绝对值的几何意义解。
因为丨×丨=5,丨y丨=1,所以×=±5,y=±1。那么丨丨×-y丨-丨× y丨丨=丨±2丨=2。因此(1)题的答案是2。
(2)从把5拆分成两个正整数的和入手。
因为丨m丨 丨n丨-5=0,得出:①m=±1,n=±4;②m=±4,n=±1;③m=±2,n=±3;④m=±3,n=±2。所以整数组(m,n)共有16组。因此2题答案是16。
例题2:
已知丨ab-2丨与丨b-1丨互为相反数,试求代数式

的值。
解题思路
运用相反数、绝对值、非负数的概念与性质,先求出a,b的值。
因为丨ab-2丨与丨b-1丨互为相反数,得:
丨ab-2丨 丨b-1丨=0,所以a=2,b=1。
把a=2,b=1代入代数式,得
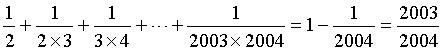
所以代数式的值是

例题3:
化简:
(1)丨2x-1丨;
(2)丨x-1丨 丨x-3丨。
解题思路
(1)就2x-1≥0,2x-1<0两种情形去掉绝对值符号。
①当x≥1/2时,丨2x-1丨=2x-1;
②当x<1/2时,丨2x-1丨=1-2x。
(2)将零点1,3(使x-1=0,3-x=0的值)在同一数轴上表示出来,就x<1,1≤x<3,x≥3三种情况进行讨论。
①当x<1时,原式=1-x 3-x=4-2x;
②当1≤x<3时,原式=x-1 3-x=2;
③当x≥3时,原式=x-1 x-3=2x-4。
综上所述,脱去绝对值符号是解绝对值问题的关键,常见的形式有:
(1)由已知条件脱去绝对值符号;
(2)从数轴上“读取”相关信息脱去绝对值符号;
(3)运用分类讨论法脱去绝对值符号。
,




